题目内容
各项均为正数的数列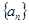 前
前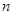 项和为
项和为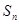 ,且
,且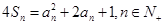 .
.
(1)求数列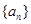 的通项公式;
的通项公式;
(2)已知公比为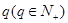 的等比数列
的等比数列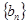 满足
满足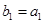 ,且存在
,且存在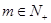 满足
满足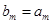 ,
,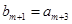 ,求数列
,求数列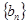 的通项公式.
的通项公式.
(1)  ;(2)
;(2) 或
或 .
.
解析试题分析:(1) ,
,
两式相减得: , (2分)
, (2分)
即
 , (4分)
, (4分) 为首项为1,公差为2的等差数列,故
为首项为1,公差为2的等差数列,故 (6分)
(6分)
(2) ,依题意得
,依题意得 ,相除得
,相除得 (8分)
(8分) ,代入上式得q=3或q=7, (10分)
,代入上式得q=3或q=7, (10分) 或
或 . (12分)
. (12分)
考点:本题主要考查等差数列、等比数列的通项公式。
点评:中档题,利用 的关系确定数列的通项公式,是常见题型,注意讨论n=1是否适合。
的关系确定数列的通项公式,是常见题型,注意讨论n=1是否适合。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
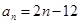 ,从数列{an}中依次取出a1,a2,a4,a8,…,
,从数列{an}中依次取出a1,a2,a4,a8,…,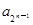 ,…,构成一个新的数列{bn},求{bn}的前n项和.
,…,构成一个新的数列{bn},求{bn}的前n项和.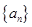 的前
的前 项和为
项和为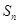 ,
,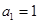 ,
,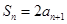 ,求
,求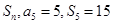 ,求数列
,求数列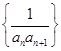 的前2012项和
的前2012项和 是等差数列,其前n项和为
是等差数列,其前n项和为 ,
, ,
, .
. 的前
的前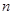 项和为
项和为 ,若
,若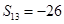 ,
,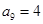 ,求:
,求: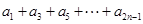 .
.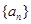 的前三项和为18,
的前三项和为18,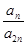 是一个与
是一个与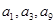 恰为等比数列
恰为等比数列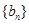 的前三项,(1)求
的前三项,(1)求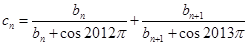 ,
,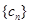 的前三
的前三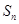 ,求证:
,求证: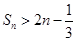
 是首项为
是首项为 ,公比
,公比 的等比数列. 设
的等比数列. 设
 ,数列
,数列 满足
满足 .
. 成等差数列;
成等差数列; 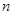 项和
项和 .
. 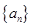 是等差数列,且
是等差数列,且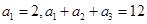
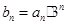 求数列
求数列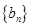 的前项n和公式
的前项n和公式 ;
;