Question

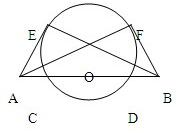半径为1的球内切于圆锥（直圆锥），已知圆锥母线与底面夹角为2θ．
（1）求证：圆锥的母线与底面半径的和是

2

tgθ(1-tg2θ)

；
（2）求证：圆锥全面积是

2π

tgθ(1-tg2θ)

；
（3）当θ是什么值时，圆锥的全面积最小？

Answer 1

分析：（1）过球心O与直圆锥底面的中心O₁作一平面与圆锥和球的截面进而可知△SAB为等腰三角形联OB，则∠OBO₁=θ设圆锥母线长为l，底面半径为R，进而可表示l和R，代入l+R中化简整理即可证明原式．
（2）把（1）中求得l和R代入圆锥的全面积=πR（l+R）中化简整理即可证明．
（3）在圆锥全面积的表达式中，因其分子为常数，所以欲使全面积最小，必须使其分母最大．进而根据正切函数的性质可知tgθ=

2

2

时，全面积最小，进而求得此时的θ．

解答：证明：（1）过球心O与直圆锥底面的中心O₁作一平面与圆锥和球的截面如图．
因此，△SAB为等腰三角形联OB，则∠OBO₁=θ
设圆锥母线长为l，底面半径为R，
则l•cos2θ=R，l=

R

cos2θ

又tan∠OBO1=

1

R

，即R=

1

tgθ

，
∴l=

1

tgθ•cos2θ

，
∴l+R=

1

tgθ•cos2θ

+

1

tgθ

=

1

tgθ

(1+

1

cos2θ

)
=

1

tgθ

•

1+cos2θ

cos2θ

=

1

tgθ

•

2cos2θ

cos2θ-sin2θ

=

1

tgθ

•

2

1-tg2θ

=

2

tgθ(1-tg2θ)

．
（2）圆锥的全面积=πR（l+R）
=π•

1

tgθ

•

2

tgθ(1-tg2θ)

=

2π

tg2θ(1-tg2θ)

．
（3）在圆锥全面积的表达式中，
因其分子为常数，
所以欲使全面积最小，
必须使其分母最大．
tg2θ(1-tg2θ)=

1

4

-

1

4

(2tg2θ-1)2．
因此，欲使tg²θ（1-tg²θ）最大，必须
2tg2θ-1=0，tgθ=

2

2

，（因必为锐，所以仅取正号）
θ=arctg

2

2

．
故当θ取值θ=arctg

2

2

时，圆锥的全面积最小．

点评：本题主要考查了组合几何体的面积和体积的问题．涉及到三角函数的性质和函数的最值问题，综合性很强．