题目内容
给出命题:若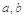 是正常数,且
是正常数,且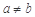 ,
,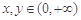 ,则
,则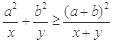 (当且仅当
(当且仅当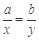 时等号成立).根据上面命题,可以得到函数
时等号成立).根据上面命题,可以得到函数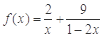 (
(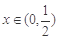 )的最小值及取最小值时的
)的最小值及取最小值时的 值分别为( )
值分别为( )
A.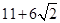 , ,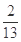 | B.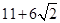 , ,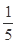 |
C.25,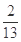 | D.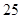 , ,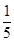 |
D
解析试题分析:本题先从给出的命题中进行学习,获取一些基本的信息,进而利用这一信息进行作答.依题意可得 ,当且仅当
,当且仅当 即
即 时等号成立,故选D.
时等号成立,故选D.
考点:创新学习题.

练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
有一段 “三段论”推理是这样的:对于可导函数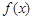 ,若
,若 ,则
,则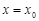 是函数
是函数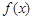 的极值点.因为
的极值点.因为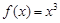 在
在 处的导数值
处的导数值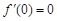 ,所以
,所以 是
是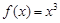 的极值点.以上推理中 ( )
的极值点.以上推理中 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
用数学归纳法证明1+2+3+ +n2=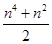 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
| A.k2+1 |
| B.(k+1)2 |
C.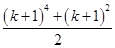 |
| D.(k2+1)+(k2+2)+ +(k+1)2 |
下面使用的类比推理中恰当的是( )
A.“若 ,则 ,则 ”类比得出“若 ”类比得出“若 ,则 ,则 ” ” |
B.“ ”类比得出“ ”类比得出“ ” ” |
C.“ ”类比得出“ ”类比得出“ ” ” |
D.“ ”类比得出“ ”类比得出“ ” ” |
根据偶函数定义可推得“函数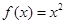 在
在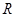 上是偶函数”的推理过程是( )
上是偶函数”的推理过程是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.非以上答案 |
用反证法证明命题:“若a,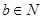 ,
,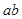 能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b有一个能被5整除 | D.a,b有一个不能被5整除 |
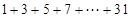 的算法,并画出相应的程序框图.
的算法,并画出相应的程序框图.
 的值为7时,则其输出的结果是 .
的值为7时,则其输出的结果是 .