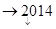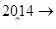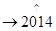题目内容
用数学归纳法证明1+2+3+ +n2=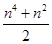 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
| A.k2+1 |
| B.(k+1)2 |
C.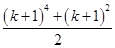 |
| D.(k2+1)+(k2+2)+ +(k+1)2 |
D
解析试题分析:当 时,
时, ,当
,当 时,
时, ,所以
,所以 时左端应在
时左端应在 的基础上加上
的基础上加上 .
.
考点:数学归纳法.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
有一段演绎推理是这样的:“直线平行于平面,则此直线平行于平面内的所有直线;已知直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 平面
平面 ,则直线
,则直线 直线
直线 ”结论显然是错误的,这是因为( )
”结论显然是错误的,这是因为( )
| A.大前提错误 | B.推理形式错误 | C.小前提错误 | D.非以上错误 |
给出命题:若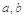 是正常数,且
是正常数,且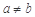 ,
,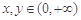 ,则
,则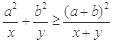 (当且仅当
(当且仅当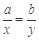 时等号成立).根据上面命题,可以得到函数
时等号成立).根据上面命题,可以得到函数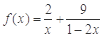 (
(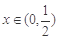 )的最小值及取最小值时的
)的最小值及取最小值时的 值分别为( )
值分别为( )
A.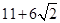 , ,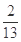 | B.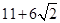 , ,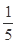 |
C.25,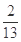 | D.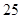 , ,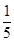 |
用反证法证明命题“三角形的内角至多有一个钝角”时,假设正确的是( )
| A.假设至少有一个钝角 | B.假设至少有两个钝角 |
| C.假设没有一个钝角 | D.假设没有一个钝角或至少有两个钝角 |
用火柴棒摆“金鱼”,如图所示: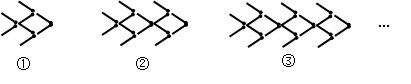
按照上面的规律,第4个“金鱼”图需要火柴棒的根数为
| A.24 | B.26 | C.28 | D.30 |
用数学归纳法证明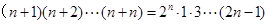 (
(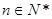 )时,从“
)时,从“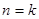 到
到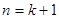 ”左边需增乘的代数式为( )
”左边需增乘的代数式为( )
A.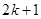 | B.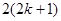 | C.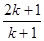 | D. |

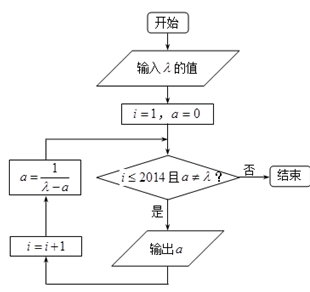
 的值依次为
的值依次为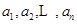 ,其中
,其中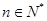 且
且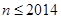 .
.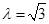 ,写出全部输出结果.
,写出全部输出结果.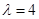 ,记
,记 ,求
,求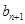 与
与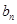 的关系(
的关系(