题目内容
已知函数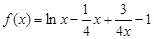 .
.
(Ⅰ)求函数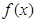 的单调区间;
的单调区间;
(Ⅱ)设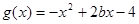 ,若对任意
,若对任意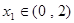 ,
,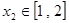 ,不等式
,不等式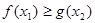 恒成立,求实数
恒成立,求实数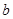 的取值范围.
的取值范围.
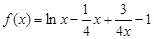 .
.(Ⅰ)求函数
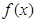 的单调区间;
的单调区间;(Ⅱ)设
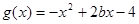 ,若对任意
,若对任意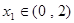 ,
,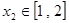 ,不等式
,不等式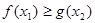 恒成立,求实数
恒成立,求实数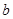 的取值范围.
的取值范围.(I)函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是
(II)b的取值范围是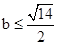
 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是
(II)b的取值范围是
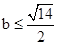
第一问利用 的定义域是
的定义域是

由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是
第二问中,若对任意 不等式
不等式 恒成立,问题等价于
恒成立,问题等价于 只需研究最值即可。
只需研究最值即可。
解: (I) 的定义域是
的定义域是 ......1分
......1分
 ............. 2分
............. 2分
由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是 ........4分
........4分
(II)若对任意 不等式
不等式 恒成立,
恒成立,
问题等价于 , .........5分
, .........5分
由(I)可知,在 上,x=1是函数极小值点,这个极小值是唯一的极值点,
上,x=1是函数极小值点,这个极小值是唯一的极值点,
故也是最小值点,所以 ; ............6分
; ............6分
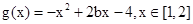
当b<1时,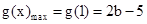 ;
;
当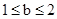 时,
时, ;
;
当b>2时,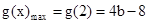 ; ............8分
; ............8分
问题等价于
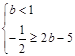 ........11分
........11分
解得b<1 或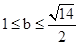 或
或 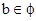 即
即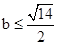 ,所以实数b的取值范围是
,所以实数b的取值范围是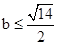
 的定义域是
的定义域是

由x>0及
 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,故函数
 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是
第二问中,若对任意
 不等式
不等式 恒成立,问题等价于
恒成立,问题等价于 只需研究最值即可。
只需研究最值即可。解: (I)
 的定义域是
的定义域是 ......1分
......1分 ............. 2分
............. 2分由x>0及
 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,故函数
 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是 ........4分
........4分(II)若对任意
 不等式
不等式 恒成立,
恒成立,问题等价于
 , .........5分
, .........5分由(I)可知,在
 上,x=1是函数极小值点,这个极小值是唯一的极值点,
上,x=1是函数极小值点,这个极小值是唯一的极值点,故也是最小值点,所以
 ; ............6分
; ............6分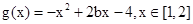
当b<1时,
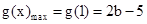 ;
;当
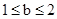 时,
时, ;
;当b>2时,
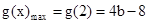 ; ............8分
; ............8分问题等价于

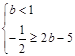 ........11分
........11分解得b<1 或
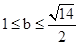 或
或 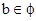 即
即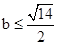 ,所以实数b的取值范围是
,所以实数b的取值范围是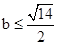

练习册系列答案
相关题目
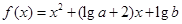 满足
满足 , 且对于任意
, 且对于任意 恒有
恒有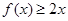 成立。
成立。 的值;
的值; 若存在实数
若存在实数 ,当
,当 时,
时,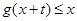 恒成立,求实数
恒成立,求实数 的最大值。
的最大值。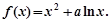
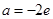 时,求函数
时,求函数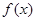 的单调区间;
的单调区间;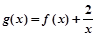 在[1,3]上是减函数,求实数
在[1,3]上是减函数,求实数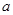 的取值范围。
的取值范围。 其中
其中 为自然对数的底数,
为自然对数的底数,  .(Ⅰ)设
.(Ⅰ)设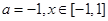 ,求函数
,求函数 的最值;(Ⅱ)若对于任意的
的最值;(Ⅱ)若对于任意的 ,都有
,都有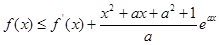 成立,求
成立,求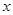 的取值范围.
的取值范围.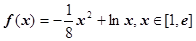
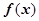 的单调区间;(Ⅱ)求
的单调区间;(Ⅱ)求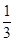 x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )
x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )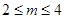
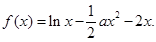
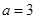 ,求
,求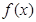 的增区间;
的增区间;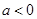 ,且函数
,且函数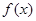 存在单调递减区间,求
存在单调递减区间,求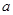 的取值范围;
的取值范围;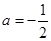 且关于
且关于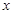 的方程
的方程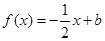 在
在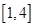 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数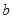 的取值范围.
的取值范围. 时,f (x)=x+sinx,设a=f (1),b=f (2),c=f (3),则( )
时,f (x)=x+sinx,设a=f (1),b=f (2),c=f (3),则( )