题目内容
3.已知向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角60°,|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2$\sqrt{3}$,$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,若λ+$\sqrt{3}$μ=2,则|$\overrightarrow{OP}$|的最小值是2$\sqrt{3}$,此时$\overrightarrow{OP}$,$\overrightarrow{OA}$夹角大小为30°.分析 由向量的数量积的定义,可得$\overrightarrow{OA}$•$\overrightarrow{OB}$=|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|•cos60°=2$\sqrt{3}$,对向量OP取模,结合向量的平方即为模的平方,运用二次函数的最值的求法,可得最小值,再由向量的夹角公式,计算即可得到所求值.
解答 解:向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角60°,|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2$\sqrt{3}$,
即有$\overrightarrow{OA}$•$\overrightarrow{OB}$=|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|•cos60°=2×2$\sqrt{3}$×$\frac{1}{2}$=2$\sqrt{3}$,
若λ+$\sqrt{3}$μ=2,可得λ=2-$\sqrt{3}$μ,
则|$\overrightarrow{OP}$|=|λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$|=$\sqrt{{λ}^{2}{\overrightarrow{OA}}^{2}+{μ}^{2}{\overrightarrow{OB}}^{2}+2λμ\overrightarrow{OA}•\overrightarrow{OB}}$
=$\sqrt{4{λ}^{2}+12{μ}^{2}+4\sqrt{3}λμ}$=$\sqrt{4(λ+\sqrt{3}μ)^{2}-4\sqrt{3}λμ}$
=$\sqrt{16-4\sqrt{3}(2-\sqrt{3}μ)μ}$=$\sqrt{12(μ-\frac{\sqrt{3}}{3})^{2}+12}$≥2$\sqrt{3}$,
当μ=$\frac{\sqrt{3}}{3}$,λ=1时,|$\overrightarrow{OP}$|的最小值为2$\sqrt{3}$;
由$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\frac{\sqrt{3}}{3}$$\overrightarrow{OB}$,
可得$\overrightarrow{OP}$•$\overrightarrow{OA}$=$\overrightarrow{OA}$2+$\frac{\sqrt{3}}{3}$$\overrightarrow{OA}$•$\overrightarrow{OB}$=4+$\frac{\sqrt{3}}{3}$•2$\sqrt{3}$=6,
则cos<$\overrightarrow{OP}$,$\overrightarrow{OA}$>=$\frac{\overrightarrow{OP}•\overrightarrow{OA}}{|\overrightarrow{OP}|•|\overrightarrow{OA}|}$=$\frac{6}{2\sqrt{3}•2}$=$\frac{\sqrt{3}}{2}$,
由0°≤<$\overrightarrow{OP}$,$\overrightarrow{OA}$>≤180°,
可得<$\overrightarrow{OP}$,$\overrightarrow{OA}$>=30°.
故答案为:2$\sqrt{3}$,30°.
点评 本题考查向量的数量积的定义和性质,以及夹角公式的运用,同时考查二次函数的最值的求法,考查运算能力,属于中档题.

| A. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | B. | -$\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ |
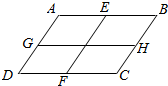 已知E,F,G,H分别是四边形ABCD四条边AB,CD,AD,BC的中点,求$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{AD}$+$\overrightarrow{DC}$=2($\overrightarrow{EF}$+$\overrightarrow{GH}$)
已知E,F,G,H分别是四边形ABCD四条边AB,CD,AD,BC的中点,求$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{AD}$+$\overrightarrow{DC}$=2($\overrightarrow{EF}$+$\overrightarrow{GH}$) 已知正方形ABCD和矩形ACEF所在的平面互相垂直,$AB=\sqrt{2}$,AF=1,M是线段EF的中点.
已知正方形ABCD和矩形ACEF所在的平面互相垂直,$AB=\sqrt{2}$,AF=1,M是线段EF的中点. 设数列{xn}的各项都为正数且x1=1.如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,若(2xn+1)$\overrightarrow{{P}_{n}C}$+$\overrightarrow{{P}_{n}A}$=$\frac{1}{3}$xn+1$\overrightarrow{{P}_{n}B}$,则x5的值为31.
设数列{xn}的各项都为正数且x1=1.如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,若(2xn+1)$\overrightarrow{{P}_{n}C}$+$\overrightarrow{{P}_{n}A}$=$\frac{1}{3}$xn+1$\overrightarrow{{P}_{n}B}$,则x5的值为31.