题目内容
16．与圆x2+（y-2）2=2相切，且在两坐标轴上的截距相等的直线方程为y=±x或y=-x+4．分析 当直线过原点时斜率存在，设方程为y=kx，当直线不过原点时，设直线的方程为y=a-x，分别联立方程由△=0可得．
解答 解：当直线过原点时斜率存在，设方程为y=kx，
联立消去y可得（k2+1）x2-4kx+2=0，
由相切可得△=16k2-8（k2+1）=0，解得k=±1，
∴所求直线的方程为y=±x；
当直线不过原点时，设直线的方程为y=a-x，
联立消去x可得2y2-（4+2a）y+a2+2=0，
由相切可得△=（4+2a）2-8（a2+2）=0，解得a=4，
∴所求直线的方程为y=-x+4
综上可得所求直线的方程为：y=±x或y=-x+4．
故答案为：y=±x或y=-x+4．
点评 本题考查直线与圆的相切关系，涉及分类讨论的思想和一元二次方程的根与判别式的关系，属中档题．
练习册系列答案
相关题目
7．已知E={θ|cosθ＜sinθ，0≤θ≤2π}，F={θ|tanθ＜sinθ}．则E∩F为（ ）
| A． | $（\frac{π}{2}，π）$ | B． | $（\frac{π}{4}，\frac{3π}{4}）$ | C． | $（π，\frac{3π}{2}）$ | D． | $（\frac{3π}{4}，\frac{5π}{4}）$ |
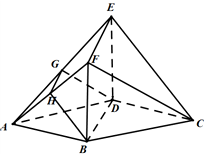如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=2，G和H分别是AE和AF的中点．
11．若tanα=2，则$\frac{sinα+cosα}{sinα-cosα}$+cos2α的值为（ ）
| A． | $\frac{7}{4}$ | B． | -$\frac{14}{5}$ | C． | $\frac{16}{5}$ | D． | $\frac{15}{4}$ |