题目内容
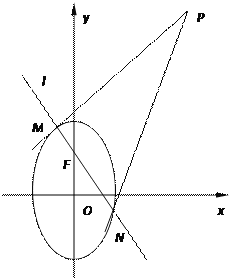
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且上焦点为
,且上焦点为![]() ,过
,过![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点.设点
两点.设点![]() ,记
,记![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 和
和![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)如果直线![]() 的斜率等于
的斜率等于![]() ,求
,求![]() 的值;
的值;
(3)探索![]() 是否为定值?如果是,求出该定值;如果不是,求出
是否为定值?如果是,求出该定值;如果不是,求出![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)2(3)
(2)2(3)![]() 为定值,且定值为2.
为定值,且定值为2.
【解析】试题分析:(1)先根据离心率以及焦点坐标列方程组,解得![]() (2)先设
(2)先设![]() 、
、![]() ,利用斜率公式化简
,利用斜率公式化简![]() 得
得![]() ,再联立直线方程与椭圆方程,利用韦达定理代入化简得
,再联立直线方程与椭圆方程,利用韦达定理代入化简得![]() 的值;(3)设直线
的值;(3)设直线![]() :
: ![]() ,同(2)化简
,同(2)化简![]() 得
得![]() ,再联立直线方程与椭圆方程,利用韦达定理代入化简得定值,最后验证斜率不存在情况也满足
,再联立直线方程与椭圆方程,利用韦达定理代入化简得定值,最后验证斜率不存在情况也满足
试题解析:解:(1)![]() ,
, ![]() ,
, ![]()
![]() ,
,
![]() 椭圆方程为
椭圆方程为![]() .
.
(2)因为直线![]() 的斜率等于
的斜率等于![]() ,且经过焦点F,
,且经过焦点F,
所以直线![]() ,
,
设![]() 、
、![]() ,
,
由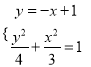 消
消![]() 得
得![]() ,
,
则有![]() ,
, ![]() .
.
所以![]() .
.
(3)当直线![]() 的斜率不存在时,
的斜率不存在时, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,故
,故![]() .
.
当直线![]() 的斜率存在时,设其为
的斜率存在时,设其为![]() ,
,
则直线![]() :
: ![]() ,
,
设![]() ,
, ![]() ,
,
由 消
消![]() 得
得![]() ,
,
则有![]() ,
, ![]() .
.
所以![]()
![]()

 .
.
所以![]() 为定值,且定值为2.
为定值,且定值为2.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中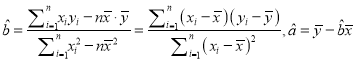 .
.