题目内容

设0＜α＜π，且函数f（x）=sin（x+α）+cos（x-α）是偶函数，则α?的值为______．
∵f（-x）=sin（-x+α）+cos（-x-α）=sinαcosx-cosαsinx+cosxcosα-sinxsinα=f（x）=sinxcosα+cosxsinα+cosxcosα+sinxsinα
∴-cosαsinx-sinxsinα=sinxcosα+sinxsinα
∴-2sinxcosα=2sinxsinα
∴sinx（sinα+cosα）=0
∴α=（2k+1）π+
π
4
，k∈Z因为0＜α＜π，所以α=
3π
4

故答案为：
3π
4
．
练习册系列答案
相关题目
设0＜a＜1，对于函数f(x)=
sinx+a
sinx
（0＜x＜π），下列结论正确的是（　　）
A、有最大值而无最小值
B、有最小值而无最大值
C、有最大值且有最小值
D、既无最大值又无最小值
（1）设0＜x＜
32
，求函数y=4x（3-2x）的最大值；
（2）已知x，y都是正实数，且x+y-3xy+5=0，求xy的最小值．
精英家教网已知函数f(x)=|
1x
-1|，其中x∈（o，+∞）．
（I）在给定的坐标系中，画出函数f（x）的图象；
（II）设0＜a＜b，且f（a）=f（b），证明：ab＞1．
已知函数f（x）=|3x-1|，g（x）=|a•3x-9|（a＞0），x∈R，且函数h(x)=
g(x)，f(x)≥g(x)
f(x)，f(x)＜g(x)

（1）当2≤a＜9时，设函数h（x）=g（x）所对应的自变量取值区间长度为d（闭区间[m，n]的长度定义为n-m），试求d的表达式并求d的最大值；
（2）是否存在这样的a，使得对任意x≥2，都有h（x）=g（x），若存在，求出a的取值范围；若不存在，请说明理由．
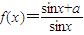设0＜a＜1，对于函数（0＜x＜π），下列结论正确的是（ ）
A．有最大值而无最小值
B．有最小值而无最大值
C．有最大值且有最小值
D．既无最大值又无最小值

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网