题目内容
设
(1)若 ,求f(x)的最小值;
,求f(x)的最小值;
(2)设g (x)= ,若g (x)有两个零点,求实数m的取值范围.
,若g (x)有两个零点,求实数m的取值范围.
解:(1)∵
=-2cos sin
sin +
+
∴ (3分)
(3分)
∵
∴x= (5分)
(5分)
(2)设g(x)= (7分)
(7分)
∵函数g(x)有两个零点
∴方程 时有两个解(9分)
时有两个解(9分)
∴y=2m与y= 图象有两个交点
图象有两个交点
则
∴ (12分)
(12分)
分析:(1)先利用诱导公式及辅助角公式对函数化简可得, ,结合正弦函数的性质可求
,结合正弦函数的性质可求
(2)由函数g(x)有两个零点可得方程 时有两个解转化为y=2m与y=
时有两个解转化为y=2m与y= 图象有两个交点,从而可求.
图象有两个交点,从而可求.
点评:诱导公式、辅助角公式一直是三角函数的常用知识,而方程的零点常转化为函数的交点问题,体现了数形结合与转化的思想在解题中的应用.

=-2cos
 sin
sin +
+
∴
 (3分)
(3分)∵

∴x=
 (5分)
(5分)(2)设g(x)=
 (7分)
(7分)∵函数g(x)有两个零点
∴方程
 时有两个解(9分)
时有两个解(9分)∴y=2m与y=
 图象有两个交点
图象有两个交点则

∴
 (12分)
(12分)分析:(1)先利用诱导公式及辅助角公式对函数化简可得,
 ,结合正弦函数的性质可求
,结合正弦函数的性质可求(2)由函数g(x)有两个零点可得方程
 时有两个解转化为y=2m与y=
时有两个解转化为y=2m与y= 图象有两个交点,从而可求.
图象有两个交点,从而可求.点评:诱导公式、辅助角公式一直是三角函数的常用知识,而方程的零点常转化为函数的交点问题,体现了数形结合与转化的思想在解题中的应用.

练习册系列答案
相关题目
 ,x∈R.
,x∈R. ,求f(x)的最大值及相应的x的集合;
,求f(x)的最大值及相应的x的集合; 是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期.
是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期.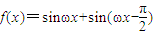 ,x∈R.
,x∈R. ,求f(x)的最大值及相应的x的集合;
,求f(x)的最大值及相应的x的集合;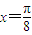 是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期.
是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期.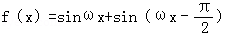 ,x∈R.
,x∈R. ,求f(x)的最大值及相应的x的集合;
,求f(x)的最大值及相应的x的集合;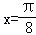 是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期.
是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期.