题目内容
设函数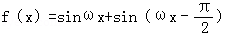 ,x∈R.
,x∈R.
(1)若ω= ,求f(x)的最大值及相应的x的集合;
,求f(x)的最大值及相应的x的集合;
(2)若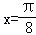 是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期.
是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期.
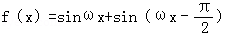 ,x∈R.
,x∈R.(1)若ω=
 ,求f(x)的最大值及相应的x的集合;
,求f(x)的最大值及相应的x的集合;(2)若
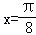 是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期.
是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期. 解:(1)f(x)=sinωx+sin(ωx﹣ )=sinωx﹣cosωx,
当ω=  时,f(x)=sin
时,f(x)=sin ﹣cos
﹣cos =
= sin(
sin( ﹣
﹣ ),
),
又﹣1≤sin( ﹣
﹣ )≤1,
)≤1,
∴f(x)的最大值为 ,
,
令 ﹣
﹣ =2kπ+
=2kπ+ ,k∈Z,
,k∈Z,
解得:x=4kπ+ ,k∈Z,
,k∈Z,
则相应的x的集合为{x|x=4kπ+ ,k∈Z};
,k∈Z};
(2)∵f(x)= sin(
sin( ﹣
﹣ ),且x=
),且x= 是f(x)的一个零点
是f(x)的一个零点
,∴f( )=sin(
)=sin( ﹣
﹣ )=0,
)=0,
∴ ﹣
﹣ =kπ,k∈Z,整理得:ω=8k+2,
=kπ,k∈Z,整理得:ω=8k+2,
又0<ω<10,∴0<8k+2<10,
解得:﹣ <k<1,又k∈Z,
<k<1,又k∈Z,
∴k=0,ω=2,
∴f(x)= sin(2x﹣
sin(2x﹣ ),
),
则f(x)的最小正周期为π.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
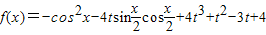 ,x∈R,其中|t|≤1,将f(x)的最小值记为g(t).
,x∈R,其中|t|≤1,将f(x)的最小值记为g(t).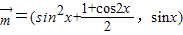 ,
,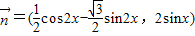 ,设函数
,设函数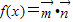 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域. ,
,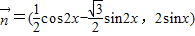 ,设函数
,设函数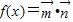 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域.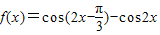 ,x∈R.
,x∈R.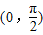 上的值域;
上的值域; ,求c的值.
,求c的值.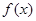 (x∈R)为奇函数,
(x∈R)为奇函数, =
= ,
, ,则
,则 =(
)
=(
)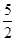 D.5
D.5