题目内容
请观察以下三个式子:
①1×3=
;
②1×3+2×4=
;
③1×3+2×4+3×5=
,
归纳出一般的结论,并用数学归纳法证明之.
①1×3=
| 1×2×9 |
| 6 |
②1×3+2×4=
| 2×3×11 |
| 6 |
③1×3+2×4+3×5=
| 3×4×13 |
| 6 |
归纳出一般的结论,并用数学归纳法证明之.
由于所给的等式的左边,是两两自然数的积再求和的形式,右边是一个分式,分母是6,分子是三个自然数的积,注意自然数与序号之间的关系,所以,猜想:1×3+2×4+3×5+…+n(n+2)=
---------(4分)
证明:(1)当n=1时,左边=3,右边=3,等式成立.
(2)假设当n=k时,等式成立,即1×3+2×4+3×5+…+k(k+2)=
------------(6分)
那么,当n=k+1时,1×3+2×4+3×5+…+k(k+2)+(k+1)(k+3)
=
+(k+1)(k+3)
=
(2k2+7k+6k+18)=
(2k2+13k+18)=
,
就是说,当 n=k+1时等式也成立.----------------------(13分)
综上所述,对任何n∈N+都成立.----------------------(14分)
| n(n+1)(2n+7) |
| 6 |
证明:(1)当n=1时,左边=3,右边=3,等式成立.
(2)假设当n=k时,等式成立,即1×3+2×4+3×5+…+k(k+2)=
| k(k+1)(2k+7) |
| 6 |
那么,当n=k+1时,1×3+2×4+3×5+…+k(k+2)+(k+1)(k+3)
=
| k(k+1)(2k+7) |
| 6 |
=
| k+1 |
| 6 |
| k+1 |
| 6 |
| (k+1)(k+2)(2k+9) |
| 6 |
就是说,当 n=k+1时等式也成立.----------------------(13分)
综上所述,对任何n∈N+都成立.----------------------(14分)

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 ;
; ;
; ,
,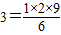 ;
;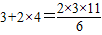 ;
; ,
,