题目内容
请观察以下三个式子:
① ;
;
② ;
;
③ ,
,
归纳出一般的结论,并用数学归纳法证明之.
【答案】

证明:①当 ,左边=3,右边=3,
,左边=3,右边=3, 左边=右边
左边=右边
②假设当 时,命题成立,
时,命题成立,
即
则当 时
时


 当
当 时命题成立,由(1)、(2)知,命题成立.
时命题成立,由(1)、(2)知,命题成立.
【解析】
试题分析: 3分
3分
证明:①当 ,左边=3,右边=3,
,左边=3,右边=3, 左边=右边
左边=右边
②假设当 时,命题成立,
时,命题成立,
即
则当 时
时


 当
当 时命题成立,由(1)、(2)知,命题成立. 10分
时命题成立,由(1)、(2)知,命题成立. 10分
考点:本题考查了数学归纳法的运用
点评:运用数学归纳法证明有关命题要注意以下几点:(1)数学归纳法的两步分别是数学归纳法的两个必要条件,二者缺一不可,两步均得以证明才具备了充分性。(2)第二步中,证明“当n=k+1时结论也正确”,必须利用归纳假设,即必须用上“当n=k(k∈N※,k≥n0)时结论正确”这一条件。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
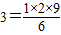 ;
;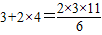 ;
; ,
,