题目内容
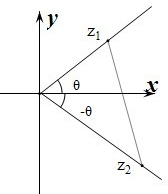设O为复平面的原点，Z1和Z2为复平面内的两动点，并且满足：（1）Z1和Z2所对应的复数的辐角分别为定值θ和-θ(0＜θ＜
| π | 2 |
（2）△OZ1Z2的面积为定值S求△OZ1Z2的重心Z所对应的复数的模的最小值．
分析：设出Z1，Z2和Z对应的复数分别为z1，z2和z，由于Z是△OZ1Z2的重心，表示其关系，求解即可．
解答：解：设Z1，Z2和Z对应的复数分别为z1，z2和z，其中
z1=r1（coθ+isinθ），
z2=r2（coθ-isinθ）．
由于Z是△OZ1Z2的重心，根据复数加法的几何意义，
则有3z=z1+z2=（r1+r2）cosθ+（r1-r2）isinθ．
于是|3z|2=（r1+r2）2cos2θ+（r1-r2）2sin2θ
=（r1-r2）2cos2θ+4r1r2cos2θ+（r1-r2）2sin2θ
=（r1-r2）2+4r1r2cos2θ
又知△OZ1Z2的面积为定值S及sin2θ＞0(0＜θ＜
)，
所以
r1r2sin2θ=S，即r1r2=
由此，|3z|2=(r1-r2)2+
=(r1-r2)2+4Sctgθ
故当r1=r2=
时，|z|最小，且|z|最小值=
．
z1=r1（coθ+isinθ），
z2=r2（coθ-isinθ）．
由于Z是△OZ1Z2的重心，根据复数加法的几何意义，
则有3z=z1+z2=（r1+r2）cosθ+（r1-r2）isinθ．
于是|3z|2=（r1+r2）2cos2θ+（r1-r2）2sin2θ
=（r1-r2）2cos2θ+4r1r2cos2θ+（r1-r2）2sin2θ
=（r1-r2）2+4r1r2cos2θ
又知△OZ1Z2的面积为定值S及sin2θ＞0(0＜θ＜
| π |
| 2 |
所以
| 1 |
| 2 |
| 2S |
| sin2θ |
由此，|3z|2=(r1-r2)2+
| 8Scos2θ |
| sin2θ |
故当r1=r2=
|
| 2 |
| 3 |
| Sctgθ |
点评：本题考查复数的基本概念，复数求模，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
设复数z=1+bi（b∈R）在复平面对应的点为Z，若|
|=2（O为复平面原点），则复数z的虚部为（ ）
| OZ |
A、
| ||
B、±
| ||
C、±
| ||
| D、±1 |
－2z1z2＋
＝0，设O为复平面原点，试判断△Z1OZ2的形状．
设O为复平面的原点，Z1和Z2为复平面内的两动点，并且满足：
；
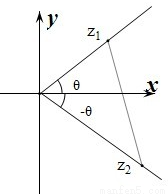设O为复平面的原点，Z1和Z2为复平面内的两动点，并且满足：
；