题目内容
已知向量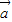 =(an,2),
=(an,2),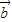 =(an+1,
=(an+1, )且a1=1,若数列{an}的前n项和为Sn,且
)且a1=1,若数列{an}的前n项和为Sn,且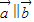 ,则Sn=( )
,则Sn=( )A.
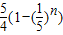
B.
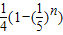
C.
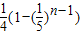
D.
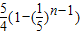
【答案】分析:由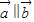 ⇒
⇒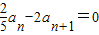 ,进一步得知数列为等比数列,运用等比数列前n项和公式计算.
,进一步得知数列为等比数列,运用等比数列前n项和公式计算.
解答:解:由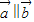 ,则
,则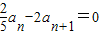 ,
,
∴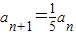 ,又a1=1,则
,又a1=1,则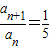 ,
,
∴数列an构成以1为首项,以 为公比的等比数列
为公比的等比数列
∴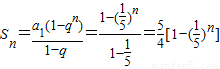 .
.
故选A.
点评:本题考查了数列的前n项和公式,解答的关键是根据向量共线,把向量坐标转化为数列递推公式,从而得出等比数列.
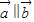 ⇒
⇒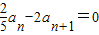 ,进一步得知数列为等比数列,运用等比数列前n项和公式计算.
,进一步得知数列为等比数列,运用等比数列前n项和公式计算.解答:解:由
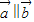 ,则
,则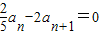 ,
,∴
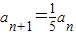 ,又a1=1,则
,又a1=1,则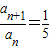 ,
,∴数列an构成以1为首项,以
 为公比的等比数列
为公比的等比数列∴
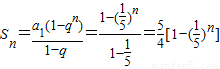 .
.故选A.
点评:本题考查了数列的前n项和公式,解答的关键是根据向量共线,把向量坐标转化为数列递推公式,从而得出等比数列.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
已知向量
=(an+1,1),
=(an+1,1),n∈N+,且a1=2,
∥
,则数列{an}的前5项和为( )
| a |
| b |
| a |
| b |
| A、10 | B、14 | C、20 | D、27 |