已知a=$0．{3}^{-\frac{1}{2}}$.b=$3．{5}^{\frac{2}{3}}$.c=$0．{3}^{-\frac{1}{3}}$.则( )A．a＞b＞cB．b＞c＞aC．a＞c＞bD．b＞a＞c 题目和参考答案——青夏教育精英家教网—

题目内容

5．已知a=$0．{3}^{-\frac{1}{2}}$，b=$3．{5}^{\frac{2}{3}}$，c=$0．{3}^{-\frac{1}{3}}$，则（　　）

A．

a＞b＞c

B．

b＞c＞a

C．

a＞c＞b

D．

b＞a＞c

分析利用指数函数的图象和性质即可得出．

解答解：∵-$\frac{1}{2}$＜$-\frac{1}{3}$，
∴2＞$0．{3}^{-\frac{1}{2}}$＞$0．{3}^{-\frac{1}{3}}$＞1，
∴2＞a＞c＞1，
∵b=$3．{5}^{\frac{2}{3}}$＞2，
∴b＞a＞c．
故选：D．

点评本题考查了指数函数的图象和性质，属于基础题．

练习册系列答案

x${\;}^{-\frac{1}{3}}$

B．

x${\;}^{\frac{2}{5}}$

C．

x${\;}^{\frac{4}{15}}$

D．

x${\;}^{-\frac{4}{15}}$

16．设△ABC的内角A、B、C所对的边分别为a、b、c，若cosB+cosC=$\frac{b+c}{a}$，则这个三角形的形状是（　　）

（0.2）^a＜（$\frac{1}{2}$）^a＜2^a

B．

（0.2）^a＜（$\frac{1}{2}$）^a＜2^a

C．

2^a＜（$\frac{1}{2}$）^a＜（0.2）^a

D．

（$\frac{1}{2}$）^a＜（0.2）^a＜2^a

20．

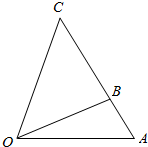在2014年亚洲移动通信博览会上，中国移动表示投资将超过2400亿元，根据规划，某地移动公司需要在如图所示的三角形地带OAC区域内建造甲、乙两个基站，甲站建立在区域BOC内，乙站建立区域AOB内，分界线OB固定，且OB=（1+$\sqrt{3}$）km，边界线AC始终过点B，∠AOC=75°，∠AOB=30°，设OA=x（3≤x≤6）km，OC=ykm
（1）试将y表示成x的函数，并求出函数y的解析式
（2）当x取何值时，两个基站的占地面积S_△OAC最小？并求出最小面积．

10．试比较下列各数的大小．
$（\frac{2}{3}）^{-\frac{1}{3}}$，$（\frac{3}{5}）^{\frac{1}{2}}$，${3}^{\frac{2}{3}}$，$（\frac{2}{5}）^{\frac{1}{2}}$，$（\frac{3}{2}）^{\frac{2}{3}}$，$（\frac{5}{6}）^{0}$，$（\frac{5}{3}）^{-\frac{2}{5}}$．

17．定义在R上的偶函数f（x）和奇函数g（x）满足f（x）+g（x）=2x，则g（2）=4．

14．f（x）=$\left\{\begin{array}{l}{{e}^{x-1}，x＞1}\\{（1-2a）x-2，x≤1}\end{array}\right.$是R上的单调函数，则a的取值范围是[-1，$\frac{1}{2}$）．

18．从某项综合能力测试中抽取100人的成绩，统计如下表，则这100人的成绩的方差为（　　）
（其中，s²=$\frac{1}{n}{\sum_{i=1}^n{（{x_i}-\overline x）}^2}$）

分数	5	4	3	2	1
人数	20	10	30	30	10

$\frac{{2\sqrt{10}}}{5}$

试题分类