题目内容
20.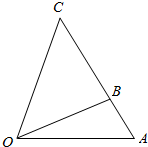 在2014年亚洲移动通信博览会上,中国移动表示投资将超过2400亿元,根据规划,某地移动公司需要在如图所示的三角形地带OAC区域内建造甲、乙两个基站,甲站建立在区域BOC内,乙站建立区域AOB内,分界线OB固定,且OB=(1+$\sqrt{3}$)km,边界线AC始终过点B,∠AOC=75°,∠AOB=30°,设OA=x(3≤x≤6)km,OC=ykm
在2014年亚洲移动通信博览会上,中国移动表示投资将超过2400亿元,根据规划,某地移动公司需要在如图所示的三角形地带OAC区域内建造甲、乙两个基站,甲站建立在区域BOC内,乙站建立区域AOB内,分界线OB固定,且OB=(1+$\sqrt{3}$)km,边界线AC始终过点B,∠AOC=75°,∠AOB=30°,设OA=x(3≤x≤6)km,OC=ykm(1)试将y表示成x的函数,并求出函数y的解析式
(2)当x取何值时,两个基站的占地面积S△OAC最小?并求出最小面积.
分析 (1)由图形知,S△BOC+S△AOB=S△AOC,代入面积公式,求出函数y的解析式;
(2)由(1)知,函数y的解析式,求出S△AOC的表达式,利用基本不等式求出S△OAC最小时,x的取值以及最小面积是什么.
解答 解:(1)结合图形可知,S△BOC+S△AOB=S△AOC.
于是,$\frac{1}{2}$x(1+$\sqrt{3}$)sin30°+$\frac{1}{2}$y(1+$\sqrt{3}$)sin45°=$\frac{1}{2}$xysin75°,
解得:y=$\frac{\sqrt{2}x}{x-2}$,(其中3≤x≤6).
(2)由(1)知,y=$\frac{\sqrt{2}x}{x-2}$(3≤x≤6),
因此,S△AOC=$\frac{1}{2}$xysin75°
=$\frac{1+\sqrt{3}}{4}$•$\frac{{x}^{2}}{x-2}$=$\frac{1+\sqrt{3}}{4}$[(x-2)+$\frac{4}{x-2}$+4]
≥2+2$\sqrt{3}$(当且仅当x-2=$\frac{4}{x-2}$,即x=4时,等号成立).
∴当x=400米时,整个中转站的占地面积S△OAC最小,最小面积是(2+2$\sqrt{3}$)×104平方米.
点评 本题考查了求函数的解析式以及利用基本不等式求函数的最值问题,解题时应根据题意,列出等量关系,求出函数的解析式,是综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.有下列四组命题:
①P:集合A⊆B,B⊆C,C⊆A,Q:集合A=B=C;
②P:A∩B=A∩C,Q:B=C;
③P:(x-2)(x-3)=0,Q:$\frac{x-2}{x-3}$=0;
④P:抛物线y=ax2+bx+c(a≠0)过原点,Q:c=0
其中P是Q的充要条件的有 ( )
①P:集合A⊆B,B⊆C,C⊆A,Q:集合A=B=C;
②P:A∩B=A∩C,Q:B=C;
③P:(x-2)(x-3)=0,Q:$\frac{x-2}{x-3}$=0;
④P:抛物线y=ax2+bx+c(a≠0)过原点,Q:c=0
其中P是Q的充要条件的有 ( )
| A. | ①、② | B. | ①、④ | C. | ②、③ | D. | ②、④ |
5.已知a=$0.{3}^{-\frac{1}{2}}$,b=$3.{5}^{\frac{2}{3}}$,c=$0.{3}^{-\frac{1}{3}}$,则( )
| A. | a>b>c | B. | b>c>a | C. | a>c>b | D. | b>a>c |
13.△ABC中,∠A=$\frac{π}{6}$,BC=1,AB=$\sqrt{2}$,则∠C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |