题目内容
设θ∈R，n∈N+，i是虚数单位，复数z=cosθ+isinθ，观察：z2=cos2θ+isin2θ，z3=cos3θ+isin3θ，…，得出一般性结论为：zn=
cosnθ+isinnθ
cosnθ+isinnθ
．分析：复数z=cosθ+isinθ，观察：z2=cos2θ+isin2θ，z3=cos3θ+isin3θ，…，得出一般性结论为：zn=cosnθ+isinnθ．可用数学归纳法证明．
解答：解：复数z=cosθ+isinθ，观察：z2=cos2θ+isin2θ，z3=cos3θ+isin3θ，…，得出一般性结论为：zn=cosnθ+isinnθ．
故答案为cosnθ+isinnθ．
可用数学归纳法证明如下：
（1）当n=1时，复数z1=cosθ+isinθ，成立；
（2）假设当n=k时，zk=coskθ+isinkθ成立，
则当n=k+1时，zk+1=zk•z=（coskθ+isinkθ）（cosθ+isinθ）=coskθcosθ-sinkθsinθ+i（coskθsinθ+sinkθcosθ）
=cos（k+1）θ+isin（k+1）θ，
因此当n=k+1时，等式成立．
综上（1）（2）可知：等式对于任何正整数n都成立．
故答案为cosnθ+isinnθ．
可用数学归纳法证明如下：
（1）当n=1时，复数z1=cosθ+isinθ，成立；
（2）假设当n=k时，zk=coskθ+isinkθ成立，
则当n=k+1时，zk+1=zk•z=（coskθ+isinkθ）（cosθ+isinθ）=coskθcosθ-sinkθsinθ+i（coskθsinθ+sinkθcosθ）
=cos（k+1）θ+isin（k+1）θ，
因此当n=k+1时，等式成立．
综上（1）（2）可知：等式对于任何正整数n都成立．
点评：本题考查了归纳推理、棣莫弗定理、数学归纳法等基础知识与基本技能方法，属于基础题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
，bn=f （bn-1） （n∈N*，n≥2），求数列{bn}的通项公式；
-1），数列{cn}的前n项和为Tn，求证：Tn＜4．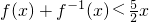
，定义数列{an}，a0=8，a1=10，an=f（an-1）（n∈N*）．
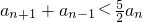（n∈N*）．
；
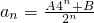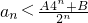．如果存在，求出A，B的值，如果不存在，说明理由．