题目内容
奇函数f(x)满足f(x+2)=f(x),当x∈(0,1)时,f(x)=2x-1,则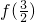 =
=
- A.-

- B.

- C.-

- D.

C
分析:先利用函数的周期为2将求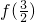 转化到区间(-1,0)内,再根据偶函数的定义和对数的运算性质求出
转化到区间(-1,0)内,再根据偶函数的定义和对数的运算性质求出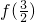 的值.
的值.
解答:∵函数f(x)是以2为周期的偶函数,
∴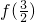 =f(-2+
=f(-2+ )=f(-
)=f(- )
)
=-f( )
)
=-
=- ,
,
故选C.
点评:本题考查了函数奇偶性和周期性的应用,根据周期性把自变量的范围转化到与题意有关的区间上,再由奇偶性联系f(x)=f(-x),利用对数的运算性质求出函数值.
分析:先利用函数的周期为2将求
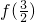 转化到区间(-1,0)内,再根据偶函数的定义和对数的运算性质求出
转化到区间(-1,0)内,再根据偶函数的定义和对数的运算性质求出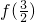 的值.
的值.解答:∵函数f(x)是以2为周期的偶函数,
∴
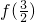 =f(-2+
=f(-2+ )=f(-
)=f(- )
)=-f(
 )
)=-

=-
 ,
,故选C.
点评:本题考查了函数奇偶性和周期性的应用,根据周期性把自变量的范围转化到与题意有关的区间上,再由奇偶性联系f(x)=f(-x),利用对数的运算性质求出函数值.

练习册系列答案
相关题目
 ,
, ,c=
,c= ,则( )
,则( )