Question

已知函数 

（1）若f(x)的定义域是R，求实数a的取值范围及f(x)的值域；

（2）若f(x)的值域是R，求实数a的取值范围及f(x)的定义域.

Answer 1

见解析。

解析:

解：（1）因为f(x)的定义域为R，所以ax2+2x+1>0对一切xR成立．

由此得解得a>1.    又因为ax2+2x+1=a(x+)+1－>0，

所以f(x)=lg(a x2+2x+1) lg(1－)，所以实数a的取值范围是(1,+ ) ,

f(x)的值域是

( 2 ) 因为f(x)的值域是R，所以u=ax2+2x+1的值域(0, +).

当a=0时，u=2x+1的值域为R(0, +)；

当a≠0时，u=ax2+2x+1的值域(0, +)等价于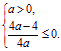

解之得0<a1.  所以实数a的取值范围是[0.1]    当a=0时，由2x+1>0得x>－,

f (x)的定义域是(－,+)；  当0<a1时，由ax2+2x+1>0

解得  

f (x)的定义域是.