题目内容
（12分）已知函数
（1）若当
的表达式；
（2）求实数
上是单调函数.
【答案】
（1）
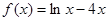；（2）
【解析】
试题分析：（1）由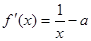
可求出f(x)的单调区间，进而得到f(x)在
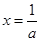处取得最大值，然后讨论
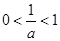和
两种情况下的最大值，最终通过解方程求出a值.
(2)先求出
,然后求导，利用导数研究其单调区间，由于含有参数a,所以应注意对a进行讨论求解.
（1）
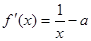
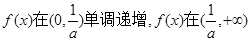单调递减，
所以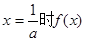
取最大值
①
解得
符合题意
②
解得
舍去
③
解得
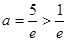舍去
综上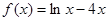
（2）
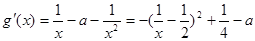
①
所以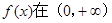
上单调递减
②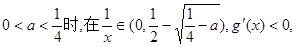
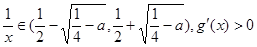
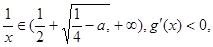
上不单调
综上
考点：导数在研究函数单调性，极值，最值当中的应用.
点评：利用导数研究单调区间，就是根据导数大（小）于零，解不等式求出其单调增（减）区间，含参时要注意对参数进行讨论，求导时还要注意函数的定义域.
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
.
(
)为函数
与
的图象的公共点，试求实数
的值； 
是函数
的图象的一条对称轴，求
的值;
的值域。
的图象上横坐标为
的点处存在垂直于y 轴的切线，求a 的值；
的图象与函数
的图象上横坐标为
的点处存在垂直于y 轴的切线，求a 的值；
的图象与函数
，求
的零点；
上有两个不同的零点，求
的取值范围。