Question

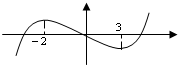（2011•乐山一模）函数f（x）=ax³+bx²+cx+d图象如右图，若函数y=ax2+

2

3

bx+

c

3

在区间[|m-1|，+∞）上单调递增，则实数m的取值范围是（　　）

• A．(-∞，

  1

  2

  ]
• B．[

  3

  2

  ，+∞)
• C．[

  3

  2

  ，+∞)∪(-∞，

  1

  2

  ]
• D．[

  1

  2

  ，

  3

  2

  ]

Answer 1

分析：由函数f（x）=ax³+bx²+cx+d图象，知-2，3是f′（x）=3ax²+2bx+c的根，且a＞0.

-2+3=- 2b 3a -2×3= c 3a

，故b=-

3

2

a，c=-18a，所以函数y=ax2+

2

3

bx+

c

3

=a（x²-x-6），由y′=2ax-a，知函数y=ax2+

2

3

bx+

c

3

的增区间是[

1

2

，+∞），故[|m-1|，+∞）⊆[

1

2

，+∞），由此能求出m的范围．

解答：解：由函数f（x）=ax³+bx²+cx+d图象，知-2，3是函数f（x）的极值点，
∴-2，3是f′（x）=3ax²+2bx+c的根，且a＞0．
∴

-2+3=- 2b 3a -2×3= c 3a

，∴b=-

3

2

a，c=-18a，
∴函数y=ax2+

2

3

bx+

c

3

=a（x²-x-6），
∴y′=2ax-a，
∵a＞0，∴由y′=2ax-a＞0，得x＞

1

2

，
∴函数y=ax2+

2

3

bx+

c

3

的增区间是[

1

2

，+∞），
∵函数y=ax2+

2

3

bx+

c

3

在区间[|m-1|，+∞）上单调递增，
∴[|m-1|，+∞）⊆[

1

2

，+∞），
解得m∈[

3

2

，+∞)∪(-∞，

1

2

]．
故选C．

点评：本题考查利用导数求闭区间上函数最值的应用，综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答，注意合理地进行等价转化．