题目内容
定义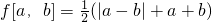 .若函数g(x)=x2-1,h(x)=x-1,则函数f[g(x),h(x)]的最小值是________.
.若函数g(x)=x2-1,h(x)=x-1,则函数f[g(x),h(x)]的最小值是________.
-1
分析:由定义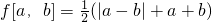 及函数g(x)=x2-1,h(x)=x-1,求出函数f[g(x),h(x)]的解析式,再求它的最小值
及函数g(x)=x2-1,h(x)=x-1,求出函数f[g(x),h(x)]的解析式,再求它的最小值
解答:∵定义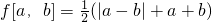 ,g(x)=x2-1,h(x)=x-1
,g(x)=x2-1,h(x)=x-1
∴f[g(x),h(x)]= =
=
∴f[g(x),h(x)]=
解得,函数的最小值是-1
故答案为-1
点评:本题考查函数的最值及其几何意义,解答本题关键是把函数的解析式求出来,由解析式求出函数的最值
分析:由定义
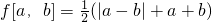 及函数g(x)=x2-1,h(x)=x-1,求出函数f[g(x),h(x)]的解析式,再求它的最小值
及函数g(x)=x2-1,h(x)=x-1,求出函数f[g(x),h(x)]的解析式,再求它的最小值解答:∵定义
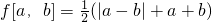 ,g(x)=x2-1,h(x)=x-1
,g(x)=x2-1,h(x)=x-1∴f[g(x),h(x)]=
 =
=
∴f[g(x),h(x)]=

解得,函数的最小值是-1
故答案为-1
点评:本题考查函数的最值及其几何意义,解答本题关键是把函数的解析式求出来,由解析式求出函数的最值

练习册系列答案
相关题目
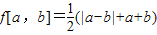 .若函数g(x)=x2-1,h(x)=x-1,则函数f[g(x),h(x)]的最小值是 .
.若函数g(x)=x2-1,h(x)=x-1,则函数f[g(x),h(x)]的最小值是 .