题目内容
设函数 在R上可导,其导函数为
在R上可导,其导函数为 ,且函数
,且函数 的图像如图所示,则下列
的图像如图所示,则下列
结论中一定成立的是( )
A.函数 有极大值 有极大值 和极小值 和极小值 |
B.函数 有极大值 有极大值 和极小值 和极小值 |
C.函数 有极大值 有极大值 和极小值 和极小值 |
D.函数 有极大值 有极大值 和极小值 和极小值 |
A
解析试题分析:由函数 的图像可知:
的图像可知: ,
, >0,
>0,  ,
, <0,
<0, ,
, >0,所以
>0,所以 在
在 ,所以函数
,所以函数 有极大值
有极大值 和极小值
和极小值 ,因此选A。
,因此选A。
考点:用导数来研究函数的单调性;用导数研究函数的极值。
点评:极值点的导数一定为零,但导数为零的点不一定是极值点。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
若函数 在
在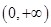 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若函数
 的图象关于直线
的图象关于直线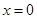 及直线
及直线 对称,且
对称,且 时,
时, ,则
,则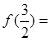 ( )
( )
A. | B. | C. | D. |
已知定义在R上的奇函数 ,满足
,满足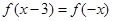 ,且在区间
,且在区间 上是增函数,若方程
上是增函数,若方程 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则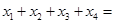
| A.6 | B. | C.18 | D.0 |
已知函数 的定义域为
的定义域为 ,
, 的定义域为
的定义域为 ,则
,则 ( )
( )
A. | B. | C. | D. |
下列函数是偶函数的是( )
A. | B. | C. | D. |
定义新运算“&”与“ ”:
”: ,
, ,则函数
,则函数
是( )
| A.奇函数 | B.偶函数 |
| C.非奇非偶函数 | D.既是奇函数又是偶函数 |
若函数y=ax+b-1(a>0且a≠1 )的图象经过一、三、四象限,则下列结论中正确的是( )
| A.a>1且b<1 | B.0<a<1 且b<0 |
| C.0<a<1 且b>0 | D.a>1 且b<0 |
 的图像大致为( )
的图像大致为( )