题目内容
曲线f(x)=x3+x-2在 点处的切线平行于直线y=4x-1,则P0点的坐标为( )
点处的切线平行于直线y=4x-1,则P0点的坐标为( )
| A.(1,0)或(-1,-4) | B.(0, 1) | C.(1,0) | D.(-1,-4) |
A
解析试题分析:设P0点的坐标为(a,f(a)),
由f(x)=x3+x-2,得到f′(x)=3x2+1,
由曲线在P0点处的切线平行于直线y=4x,得到切线方程的斜率为4,
即f′(a)=3a2+1=4,解得a=1或a=-1,
当a=1时,f(1)=0;当a=-1时,f(-1)=-4,
则P0点的坐标为(1,0)或(-1,-4).故选A.
考点:本题主要考查导数的几何意义.
点评:中档题,研究曲线上某点切线方程时,要注意已知是否给定切点。函数在某点的导数值等于以该点为切点的切线的斜率。

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 等于
等于
| A.1 | B.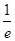 | C. | D. |
已知函数 在(1,4)上是减函数,则实数
在(1,4)上是减函数,则实数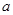 的取值范围是( )
的取值范围是( )
A. | B.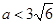 | C. | D. |
已知 为
为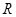 上的可导函数,且
上的可导函数,且 ,均有
,均有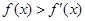 ,则有( )
,则有( )
A. |
B. |
C. |
D. |
函数 在闭区间[-3,0]上的最大值、最小值分别是( )
在闭区间[-3,0]上的最大值、最小值分别是( )
| A.1,-1 | B. 3,-17 | C. 1,-17 | D.9,-19 |
当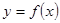 是下列的( )时,f ′(x)一定是增函数。
是下列的( )时,f ′(x)一定是增函数。
| A.二次函数 | B.反比例函数 | C.对数函数 | D.指数函数 |
已知函数 ,则
,则 ( )
( )
| A.-1 | B.-3 | C.2 | D.-2 |
设连续函数 ,则当
,则当 时,定积分
时,定积分 的符号( )
的符号( )
| A.一定是正的 |
| B.一定是负的 |
C.当 时是正的,当 时是正的,当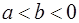 时是负的 时是负的 |
| D.以上结论都不对 |
对于R上可导的任意函数f(x),若满足(x-1)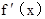 ³0,则必有( )
³0,则必有( )
| A.f(0)+f(2)<2f(1) | B.f(0)+f(2)£2f(1) |
| C. f(0)+f(2)³2f(1) | D.f(0)+f(2)>2f(1) |