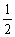题目内容
(22)如图,P是抛物线C:y=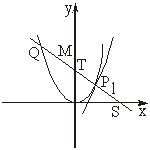
(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求![]() +
+![]() 的取值范围.
的取值范围.
(22)本小题主要考查直线、抛物线、不等式等基础知识,求轨迹方程的方法,解析几何的基本思想和综合解题能力.

解:
(Ⅰ)设P(x1,y1),Q(x2,y2),M(x0,y0),依题意x1≠0,y1>0,y2>0.
由y=![]() x2, ①
x2, ①
得y′=x.
∴过点P的切线的斜率k切=x1.
∵x1=0不合题意,∴x1≠0.
∴直线l的斜率kl=-![]() =-
=-![]() ,
,
直线l的方程为y-![]() x12=-
x12=-![]() (x-x1). ②
(x-x1). ②
方法一:
联立①②消去y,得x2+![]() -x12-2=0.
-x12-2=0.
∵M为PQ的中点,
∴
消去x1,得y0=x02+![]() +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+![]() +1(x≠0).
+1(x≠0).
方法二:
由y1=![]() x12,y2=
x12,y2=![]() x22,x0=
x22,x0=![]() ,
,
得y1-y2=![]() x12-
x12-![]() x22=
x22=![]() (x1+x2)(x1-x2)=x0(x1-x2),
(x1+x2)(x1-x2)=x0(x1-x2),
则x0=![]() =kl=-
=kl=-![]() ,
,
∴x1=-![]() ,
,
将上式代入②并整理,得
y0=x02+![]() +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+![]() +1(x≠0).
+1(x≠0).
(Ⅱ)设直线l:y=kx+b,依题意k≠0,b≠0,则T(0,b).
分别过P、Q作PP′⊥x轴,QQ′⊥y轴,垂足分别为P′、Q′,则
![]() +
+![]() =
=![]() +
+![]() =
=![]() +
+![]() .
.

方法一:
∴![]() +
+![]() =|b|(
=|b|(![]() +
+![]() )≥2|b|
)≥2|b|![]() =2|b|
=2|b|![]() =2.
=2.
∵y1、y2可取一切不相等的正数,
∴![]() +
+![]() 的取值范围是(2,+∞).
的取值范围是(2,+∞).
方法二:
∴![]() +
+![]() =|b|
=|b|![]() =|b|
=|b|![]() .
.
当b>0时, ![]() +
+![]() =b
=b![]() =
=![]() =
=![]() +2>2;
+2>2;
当b<0时, ![]() +
+![]() =-b
=-b![]() =
=![]() .
.
又由方程③有两个相异实根,得Δ=4(k2+b)2-4b2=4k2(k2+2b)>0,
于是k2+2b>0,即k2>-2b.
所以![]() +
+![]() >
>![]() =2.
=2.
∵当b>0时,![]() 可取一切正数,
可取一切正数,
∴![]() +
+![]() 的取值范围是(2,+∞).
的取值范围是(2,+∞).
方法三:
由P、Q、T三点共线得kTQ=kTP,
即![]() =
=![]() .
.
则x1y2-bx1=x2y1-bx2,即b(x2-x1)=(x2y1-x1y2).
于是b= =-
=-![]() x1x2.
x1x2.
∴![]() +
+![]() =
=![]() +
+![]() =
= +
+ =
=![]() +
+![]() ≥2.
≥2.
∵![]() 可取一切不等于1的正数,
可取一切不等于1的正数,
∴![]() +
+![]() 的取值范围是(2,+∞).
的取值范围是(2,+∞).

 阅读快车系列答案
阅读快车系列答案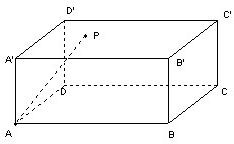 如图P是长方体AC′上底面内的一点,设AP与三个面A′C′、面A′B、面A′D所成的角为α,β,γ,则cos2α+cos2β+cos2γ=( )
如图P是长方体AC′上底面内的一点,设AP与三个面A′C′、面A′B、面A′D所成的角为α,β,γ,则cos2α+cos2β+cos2γ=( )| A、1 | ||
| B、2 | ||
C、
| ||
| D、随着P点的位置而定 |
 如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.其中Q是PB中点,S是AB的中点.求证:
如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.其中Q是PB中点,S是AB的中点.求证: