题目内容
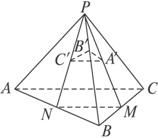
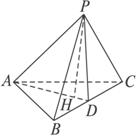
 如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.其中Q是PB中点,S是AB的中点.求证:
如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.其中Q是PB中点,S是AB的中点.求证:(1)AB⊥平面MNQ
(2)MN⊥AB.
分析:(1)依题意,连结MQ,NQ,可证MQ⊥平面PAB,从而可得MQ⊥AB,再利用PA=PB,AN=3NB,S是AB的中点可证得QN⊥AB,利用线面垂直的判定定理即可证得结论;
(2)利用线面垂直的性质定理即可.
(2)利用线面垂直的性质定理即可.
解答: 证明:(1)∵PB的中点为Q,连结MQ,NQ,
证明:(1)∵PB的中点为Q,连结MQ,NQ,
∵M是PC的中点,
∴MQ∥BC,
∵CB⊥平面PAB,
∴MQ⊥平面PAB,
∴MQ⊥AB,①
又S是AB的中点,连结QS,则QS∥PA;
∵PA=PB,
∴PS⊥AB;
∴又AN=3NB,
∴BN=NS,
∴QN∥PS,
∴QN⊥AB,②
MQ∩QN=Q,③
由①②③知AB⊥平面QMN;
(2)由(1)知AB⊥平面QMN,又MN?平面QMN,
∴MN⊥AB.
 证明:(1)∵PB的中点为Q,连结MQ,NQ,
证明:(1)∵PB的中点为Q,连结MQ,NQ,∵M是PC的中点,
∴MQ∥BC,
∵CB⊥平面PAB,
∴MQ⊥平面PAB,
∴MQ⊥AB,①
又S是AB的中点,连结QS,则QS∥PA;
∵PA=PB,
∴PS⊥AB;
∴又AN=3NB,
∴BN=NS,
∴QN∥PS,
∴QN⊥AB,②
MQ∩QN=Q,③
由①②③知AB⊥平面QMN;
(2)由(1)知AB⊥平面QMN,又MN?平面QMN,
∴MN⊥AB.
点评:本题考查直线与平面垂直的判定定理与性质定理的应用,考查推理、证明的能力,属于中档题.

练习册系列答案
相关题目