题目内容

设m为实数，A(tana，0)，B(tanb，0)是二次函数f(x)=mx2+(2m-3)x+m-2图象上的两点，求函数y=tan(a+b)的最小值

 

答案：
解析：

因为A(tana，0)，B(tanb，0)是二次函数y=mx2+(2m-3)x+m-2图象上的两点，所以tana，tanb是二次方程mx2+(2m-3)x+m-2=0的两个实数根，

所以

解得。

根据韦达定理，得tana+tanb=，tanatanb=。

所以tan(a+b)=。

所以当时，tan(a+b)有最小值。

 


练习册系列答案
相关题目
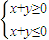已知向量
a
、
b
的夹角为60°，且|
a
|=1，|
b
|=2，设
m
=3
a
-
b
，
n
=t
a
+2
b

（1）若
m
⊥
n
，求实数t的值；
（2）当t=2时，求
m
与
n
的夹角．
已知向量
a
，
b
的夹角为60°，且|
a
|=1，|
b
|=2，设
m
=3
a
-
b
，
n
=t
a
+2
b

（1）求
a
•
b
；  （2）试用t来表示
m
•
n
的值；（3）若
m
与
n
的夹角为钝角，试求实数t的取值范围．
设M为平面内一些向量组成的集合，若对任意正实数t和向量a∈M，都有ta∈M，则称M为“点射域”．现有下列平面向量的集合：
①{（x，y）|x2≥y}；
②{（x，y）|
x+y≥0
x+y≤0
}；
③{（x，y）|x2+y2-2x≥0}；
④{（x，y）|3x2+2y2-6＜0}．
上述为“点射域”的集合有
②
②
（写出所有正确命题的序号）．
设M为平面内一些向量组成的集合，若对任意正实数t和向量a∈M，都有ta∈M，则称M为“点射域”．现有下列平面向量的集合：
①{（x，y）|x2≥y}；
②{（x，y）|
x+y≥0
x+y≤0
}；
③{（x，y）|x2+y2-2x≥0}；
④{（x，y）|3x2+2y2-6＜0}．
上述为“点射域”的集合有______（写出所有正确命题的序号）．
设M为平面内一些向量组成的集合，若对任意正实数t和向量a∈M，都有ta∈M，则称M为“点射域”．现有下列平面向量的集合：
①{（x，y）|x2≥y}；
②{（x，y）|}；
③{（x，y）|x2+y2-2x≥0}；
④{（x，y）|3x2+2y2-6＜0}．
上述为“点射域”的集合有    （写出所有正确命题的序号）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网