题目内容
(20)如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥CD,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=![]() ,PB⊥PD.
,PB⊥PD.

(Ⅰ)求异面直线PD与BC所成角的余弦值;
(Ⅱ)求二面角P-AB-C的大小;
(Ⅲ)设点M在棱PC上,且![]() 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.
解法一:
∵PO⊥平面ABCD,∴PO⊥BD.
又PB⊥PD,BO=2,PO=![]() ,
,
由平面几何知识得: OD=1,PD=![]() ,PB=
,PB=![]() .
.
(Ⅰ)过D作DE∥BC交于AB于E.连结PE,则
∠PDE或其补角为异面直线PD与BC所成的角.

∵四边形ABCD是等腰梯形,
∴OC=OD=1,OB=OA=2,OA⊥OB,
∴BC=![]() ,AB=2
,AB=2![]() ,CD=
,CD=![]()
又AB∥DC,
∴四边形EBCD是平行四边形.
∴ED=BC=![]() ,BE=CD=
,BE=CD=![]() .
.
∴E是AB的中点,且AE=![]() .
.
又PA=PB=![]() ,
,
∴△PEA为直角三角形.
∴PE=![]() .
.
在△PED中,由余弦定理得:
cos∠PDE=![]()
![]() .
.
故异面直线PD与BC所成的角的余弦值为![]() .
.
(Ⅱ)连结OE,由(Ⅰ)及三垂线定理知,∠PEO为二面角P-AB-C的平面角.
∴sin∠PEO=![]() ,
,
∴∠PEO=45°.
∴二面角P-AB-C的大小为45°.
(Ⅲ)连结MD,MB,MO,

∵PC⊥平面BMD,OM![]() 平面BMD,
平面BMD,
∴PC⊥OM.
又在Rt△POC中,
PC=PD=![]() ,OC=1,PO=
,OC=1,PO=![]() ,
,
∴PM=![]() ,MC=
,MC=![]() ,
,
∴![]() =2.
=2.
故λ=2时,PC⊥平面BMD.
解法二:

∵PO⊥平面ABCD,
∴PO⊥BD.
又PB⊥PD,BO=2,PO=![]() ,
,
由平面几何知识得:
OD=OC=1,BO=AO=2.
以O为原点,OA,OB,OP分别为x,y,z轴建立如图所示的空间直角坐标系,则各点坐标为O(0,0,0),A(2,0,0),B(0,2,0),C(-1,0,0),D(0,-1,0),P(0,0,![]() ).
).
(Ⅰ)∵![]() =(0,-1,-
=(0,-1,-![]() ),
),![]() =(-1,-2,0),
=(-1,-2,0),
∴|![]() |=
|=![]() ,|
,|![]() |=
|=![]() ,
,![]() ·
·![]() =2.
=2.

=![]()
故直线PD与BC所成的角的余弦值为![]() .
.
(Ⅱ)设平面PAB的一个法向量为n=(x,y,z),
由于![]() =(-2,2,0),
=(-2,2,0),![]() =(-2,0,
=(-2,0,![]() ),
),
由
得 
取n=(1,1,![]() ),又易知平面ABCD的一个法向量m=(0,0,1),
),又易知平面ABCD的一个法向量m=(0,0,1),
![]()
又二面角P-AB-C为锐角,
∴所求二面角P-AB-C的大小为45°.
(Ⅲ)设M(x0,0,z0),由于P,M,C三点共线,
z0=![]() x0+
x0+![]() (1)
(1)
∵PC⊥平面BMD,
∴OM⊥PC.
∴(-1,0,-![]() )·(x0,0,z0)=0
)·(x0,0,z0)=0
∴x0+![]() z0=0 (2)
z0=0 (2)
由(1)(2)知:
x0=-![]() ,z0=
,z0=![]() .
.
∴M(-![]() ,0,
,0,![]() ).
).
∴λ=![]() =2.
=2.
故λ=2时,PC⊥平面BMD.

 阅读快车系列答案
阅读快车系列答案 4、某校对高三年级的学生进行体检,现将高三男生的体重(单位:kg)数据进行整理后分成五组,并绘制频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65 kg属于偏胖,低于55 kg属于偏瘦.已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05,第二小组的频数为400,则该校高三年级的男生总数和体重正常的频率分别为( )
4、某校对高三年级的学生进行体检,现将高三男生的体重(单位:kg)数据进行整理后分成五组,并绘制频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65 kg属于偏胖,低于55 kg属于偏瘦.已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05,第二小组的频数为400,则该校高三年级的男生总数和体重正常的频率分别为( ) [选做题]在下面A,B,C,D四个小题中只能选做两题,每小题10分,共20分.
[选做题]在下面A,B,C,D四个小题中只能选做两题,每小题10分,共20分. (2012•湖北)某个实心零部件的形状是如图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD,上不是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱ABCD-A2B2C2D2.
(2012•湖北)某个实心零部件的形状是如图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD,上不是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱ABCD-A2B2C2D2.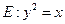
 与圆
与圆 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。