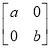
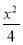题目内容
已知直线l:y=x+m,m∈R.
(1)若以点M(2,0)为圆心的圆与直线l相切于点P,且点P在y轴上,求该圆的方程;
(2)若直线l关于x轴对称的直线为l′,问直线l′与抛物线C:x2=4y是否相切?说明理由.
(1)(x-2)2+y2=8.(2)当m=1时,直线l′与抛物线C相切.
当m≠1时,直线l′与抛物线C不相切
【解析】法一:(1)依题意,点P的坐标为(0,m).
因为MP⊥l,
所以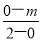 ×1=-1,
×1=-1,
解得m=2,即点P的坐标为(0,2).
从而圆的半径r=|MP|=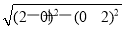 =2
=2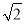 .?
.?
故所求圆的方程为(x-2)2+y2=8.
(2)因为直线l的方程为y=x+m,
所以直线l′的方程为y=-x-m.
由 得x2+4x+4m=0.
得x2+4x+4m=0.
Δ=42-4×4m=16(1-m).
①当m=1,即Δ=0时,直线l′与抛物线C相切;
②当m≠1,即Δ≠0时,直线l′与抛物线C不相切.
综上,
.
法二(1)设所求圆的半径为r,
则圆的方程可设为(x-2)2+y2=r2.
依题意,所求圆与直线l:x-y+m=0相切于点P(0,m),
则 解得
解得
所以所求圆的方程为(x-2)2+y2=8.
(2)同法一.

练习册系列答案
相关题目