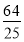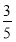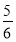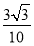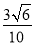题目内容
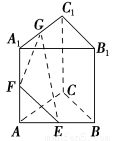
已知四边形ABCD是菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,G,H分别是CE,CF的中点.

(1)求证:平面AEF∥平面BDGH
(2)若平面BDGH与平面ABCD所成的角为60°,求直线CF与平面BDGH所成的角的正弦值.
(1)见解析(2)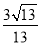
【解析】(1)G,H分别为CE,CF的中点,
所以EF∥GH,
连接AC与BD交于O,因为四边形ABCD是菱形,所以O是AC的中点,
连接OG,OG是三角形ACE的中位线,OG∥AE,
又EF∩AE=E,GH∩OG=G,则平面AEF∥平面BDGH,
(2)因为BF⊥BD,平面BDEF⊥平面ABCD,
所以BF⊥平面ABCD,
取EF的中点N,连接ON,则ON∥BF,∴ON⊥平面ABCD,
建立空间直角坐标系如图所示,设AB=2,BF=t,

则B(1,0,0),C(0,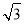 ,0),F(1,0,t),
,0),F(1,0,t),
H ,
,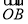 =(1,0,0),
=(1,0,0),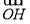 =
= ,
,
设平面BDGH的法向量为n1=(x,y,z),
 取n1=(0,-t,
取n1=(0,-t,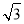 ),
),
平面ABCD的法向量n2=(0,0,1),
|cos〈n1,n2〉|=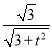 =
= ,所以t2=9,t=3.
,所以t2=9,t=3.
所以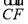 =(1,-
=(1,- ,3),设直线CF与平面BDGH所成的角为θ,
,3),设直线CF与平面BDGH所成的角为θ,
sin θ=|cos〈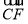 ,n1〉|=
,n1〉|=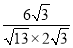 =
= .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目