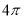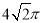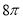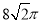Question

在正三棱锥S-ABC中，外接球的表面积为，M，N分别是SC,BC的中点，且,则此三棱锥侧棱SA=（ ）

（A）1 (B) 2 (C) (D)

 

Answer 1

D

【解析】

试题分析：作SO⊥平面ABC，O为三角形ABC的重心. 平面ABC，SO⊥AC. 作BO交AC于点D.所以AC⊥BD.又.所以AC⊥SB.又因为M,N分别是中点，所以MN∥SB，又因为MN⊥AM.所以AM⊥SB.又因为.所以SB⊥平面SAC.又因为三棱锥S-ABC是正三棱锥，所以SA,SB,SC之间两两垂直.通过补齐为一个正方体，则正方体的外接球的直径为6，则正方体的棱长为.满足.故选D.

考点：1.球的表面积.2.割补法的思想.3.线线、线面位置关系.