题目内容
如图(1) 是等腰直角三角形,其中
是等腰直角三角形,其中 ,
, 分别为
分别为 的中点,将
的中点,将 沿
沿 折起,点
折起,点 的位置变为点
的位置变为点 ,已知点
,已知点 在平面
在平面 上的射影
上的射影 为
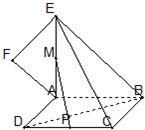
为 的中点,如图(2)所示.
的中点,如图(2)所示.

(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
【答案】
(Ⅰ) 是等腰直角
是等腰直角 的中位线,
的中位线, ,由
,由 ,
, ,
, 平面
平面
 (Ⅱ)
(Ⅱ)
【解析】
试题分析:(I)证法一:在 中,
中, 是等腰直角
是等腰直角 的中位线,
的中位线,
在四棱锥 中,
中, ,
, ,
,  平面
平面 ,
,
又 平面
平面 ,
,  6分
6分
证法二:同证法一

 平面
平面 ,
,
又 平面
平面 ,
,  6分
6分
(Ⅱ)在直角梯形 中 ,
中 ,
 ,
, 
 =
=
又 垂直平分
垂直平分 ,
, 9分
9分
 三棱锥
三棱锥 的体积为:
的体积为:
考点:线面垂直的判定和性质及三棱锥体积
点评:当直线垂直于平面内两相交直线时直线垂直于平面,第二问求三棱锥体积选用合适的底面使底面积和高都易求出,要注意这一技巧

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,正方形ABCD所在平面与平面四边形ABEF所在的平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.
如图,正方形ABCD所在平面与平面四边形ABEF所在的平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.

 是等腰直角三角形,
是等腰直角三角形, 是
是

 面
面 ;
; 和
和