题目内容
已知 ,命题
,命题 函数
函数 在
在 上单调递减,命题
上单调递减,命题 曲线
曲线 与
与 轴交于不同的两点,若
轴交于不同的两点,若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围。
的取值范围。
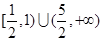
解析试题分析:根据对数函数的单调性我们易判断出命题p为真命题时参数a的取值范围,及命题p为假命题时参数a的取值范围;根据二次函数零点个数的确定方法,我们易判断出命题q为真命题时参数a的取值范围,及命题q为假命题时参数a的取值范围;由p且q为假命题,p或q为真命题,我们易得到p与q一真一假,分类讨论,分别构造关于x的不等式组,解不等式组即可得到答案.
解: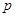 为真:
为真: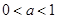 ; 2分;
; 2分;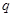 为真:
为真: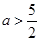 或
或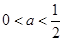 4分
4分
因为 为假命题,
为假命题, 为真命题,所以
为真命题,所以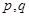 命题一真一假 5分
命题一真一假 5分
(1)当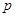 真
真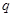 假
假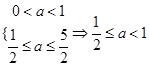 7分
7分
(2)当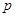 假
假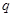 真
真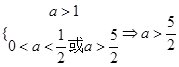 9分
9分
综上, 的取值范围是
的取值范围是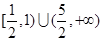 10分
10分
考点:1.复合命题的真假的判断;2.函数的性质.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
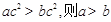 ”的逆命题; ④若“
”的逆命题; ④若“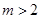 ,
,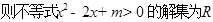 ”
” :函数y=kx+1在R上是增函数,命题
:函数y=kx+1在R上是增函数,命题 :曲线
:曲线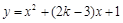 与x轴交于不同的两点,如果
与x轴交于不同的两点,如果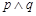 是假命题,
是假命题, 是真命题,求k的取值范围.
是真命题,求k的取值范围.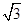 ,这个条件是其充分条件吗?为什么?
,这个条件是其充分条件吗?为什么?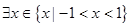 ,使等式
,使等式 成立”是真命题.
成立”是真命题. 的取值集合
的取值集合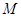 ;
; 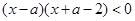 的解集为
的解集为 ,若
,若 是
是 的必要条件,求
的必要条件,求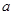 的取值范围.
的取值范围.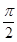 ,试判断p∨q,p∧q,
,试判断p∨q,p∧q,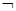 p的真假性.
p的真假性.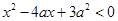 ,其中
,其中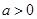 ,命题
,命题 实数
实数 满足
满足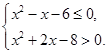 .
. 且
且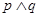 为真,求实数
为真,求实数 是
是
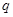 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围. : 关于
: 关于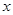 的不等式
的不等式 ,对一切
,对一切 恒成立; 命题
恒成立; 命题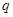 : 函数
: 函数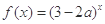 在
在 上是增函数.若
上是增函数.若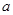 的取值范围.
的取值范围.