题目内容
设 、
、 、
、 为非零向量,下列等恒成立的个数有
为非零向量,下列等恒成立的个数有
①( •
• )•
)• =(
=( •
• )•
)• ;②[(
;②[( •
• )•
)• -(
-( •
• )•
)• ]•
]• =0;
=0;
③ 2-
2- 2=(
2=( +
+ )(
)( -
- );④
);④ +
+ =(
=( +
+ )(
)( -
- •
• +
+ ).
).
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:在( •
• )•
)• =(
=( •
• )•
)• 中,(
中,( •
• )与(
)与( •
• )是实数,而
)是实数,而 ,
, 方向可能不同,故①式不一定成立;由向量的数量积运算法则,可验证②式成立,同理,也可验证③④成立.
方向可能不同,故①式不一定成立;由向量的数量积运算法则,可验证②式成立,同理,也可验证③④成立.
解答:(1)设( •
• )•
)• =λ
=λ ,(
,( •
• )•
)• =λ'
=λ' (其中λ,λ'∈R),
(其中λ,λ'∈R), ,
, 方向可能不同,故①式不一定成立;
方向可能不同,故①式不一定成立;
(2)∵[( •
• )•
)• -(
-( •
• )•
)• ]•
]• =(
=( •
• )•(
)•( •
• )-(
)-( •
• )•(
)•( •
• )=0,∴②式恒成立;
)=0,∴②式恒成立;
(3)∵( +
+ )(
)( -
- )=
)= -
- •
• +
+ •
• -
- =
= -
- ,∴③式恒成立;
,∴③式恒成立;
(4)∵( +
+ )(
)( -
- •
• +
+ )=
)= -
- •
• •
• +
+
 +
+ •
• -
- •
• •
• +
+ =
= +
+ ,∴④式恒成立;
,∴④式恒成立;
故选C.
点评:本题考查了平面向量数量积的定义,数量积的运算法则及其应用,是基础题.
分析:在(
 •
• )•
)• =(
=( •
• )•
)• 中,(
中,( •
• )与(
)与( •
• )是实数,而
)是实数,而 ,
, 方向可能不同,故①式不一定成立;由向量的数量积运算法则,可验证②式成立,同理,也可验证③④成立.
方向可能不同,故①式不一定成立;由向量的数量积运算法则,可验证②式成立,同理,也可验证③④成立.解答:(1)设(
 •
• )•
)• =λ
=λ ,(
,( •
• )•
)• =λ'
=λ' (其中λ,λ'∈R),
(其中λ,λ'∈R), ,
, 方向可能不同,故①式不一定成立;
方向可能不同,故①式不一定成立;(2)∵[(
 •
• )•
)• -(
-( •
• )•
)• ]•
]• =(
=( •
• )•(
)•( •
• )-(
)-( •
• )•(
)•( •
• )=0,∴②式恒成立;
)=0,∴②式恒成立;(3)∵(
 +
+ )(
)( -
- )=
)= -
- •
• +
+ •
• -
- =
= -
- ,∴③式恒成立;
,∴③式恒成立;(4)∵(
 +
+ )(
)( -
- •
• +
+ )=
)= -
- •
• •
• +
+
 +
+ •
• -
- •
• •
• +
+ =
= +
+ ,∴④式恒成立;
,∴④式恒成立;故选C.
点评:本题考查了平面向量数量积的定义,数量积的运算法则及其应用,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
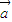 ,
,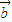 是两个非零向量,则“向量
是两个非零向量,则“向量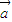 ,
,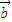 的夹角为锐角”是“函数f(x)=(x
的夹角为锐角”是“函数f(x)=(x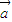 +
+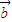 )•(
)•(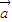 -x
-x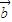 )的图象是一条开口向下的抛物线”的( )
)的图象是一条开口向下的抛物线”的( )