题目内容
(本小题满分12分)椭圆C的中心为坐标原点O,焦点在y轴上,短轴长为 、离心率为
、离心率为 ,直线
,直线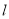 与y轴交于点P(0,
与y轴交于点P(0,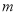 ),与椭圆C交于相异两点A、B,且
),与椭圆C交于相异两点A、B,且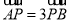 。
。
(Ⅰ)求椭圆方程;
(Ⅱ)求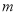 的取值范围。
的取值范围。
(Ⅰ)
(Ⅱ)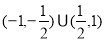
【解析】
试题分析:第一问中由短轴长可以求出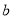 的值,根据椭圆的离心率,可以得出
的值,根据椭圆的离心率,可以得出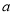 和
和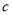 的值,从而得出椭圆的方程,对于第二问,先将直线的方程设出来,与椭圆的方程联立,消元,设出两个交点的坐标,根据向量的关系,得出两个坐标之间的关系,从而得到方程两个根之间的关系,再根据韦达定理,找出关于斜率和截距的关系式,由方程有两个根,应用判别式大于零,找出相应的不等式,从而求出结果.
的值,从而得出椭圆的方程,对于第二问,先将直线的方程设出来,与椭圆的方程联立,消元,设出两个交点的坐标,根据向量的关系,得出两个坐标之间的关系,从而得到方程两个根之间的关系,再根据韦达定理,找出关于斜率和截距的关系式,由方程有两个根,应用判别式大于零,找出相应的不等式,从而求出结果.
试题解析:(I)设C: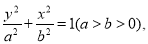 设
设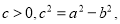
由条件知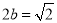 ,
,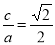 ,
,
∴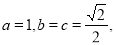 3分
3分
故C的方程为: 4分
4分
(Ⅱ)设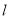 与椭圆C交点为A(
与椭圆C交点为A(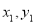 ),B(
),B(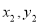 )
)
由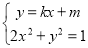 得
得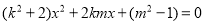
得(k2+2)x2+2kmx+(m2-1)=0
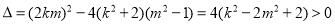 (*)
(*)
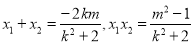 8分
8分
∵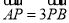 ∴
∴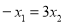 ∴
∴
消去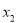 ,得
,得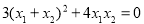 ,∴
,∴
整理得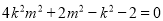 10分
10分
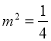 时,上式不成立;
时,上式不成立; 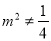 时,
时,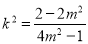 ,
,
由(*)式得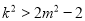
因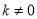 ∴
∴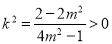 ,∴
,∴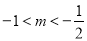 或
或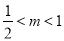
即所求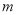 的取值范围为
的取值范围为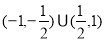 12分
12分
考点:椭圆的方程,直线与椭圆相交问题的转换,向量的坐标关系.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
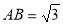 ,
,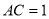 ,∠A=30°,则△ABC面积为 ( )
,∠A=30°,则△ABC面积为 ( )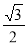 B.
B.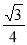 C.
C.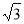 D.
D.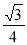 或
或 ,b=
,b= ,c=
,c= , 则( )
, 则( )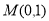 与抛物线
与抛物线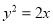 只有一个公共点的直线有( )
只有一个公共点的直线有( ) 的准线方程是( )
的准线方程是( ) B.
B. C.
C. D.
D.
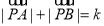 ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;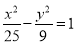 与椭圆
与椭圆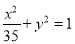 有相同的焦点;
有相同的焦点;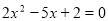 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;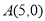 及定直线
及定直线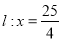 的距离之比为
的距离之比为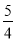 的点的轨迹方程为
的点的轨迹方程为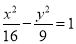 .
.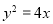 焦点的直线交抛物线于
焦点的直线交抛物线于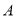 ,
,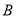 两点,若
两点,若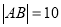 ,则
,则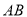 的中点到
的中点到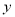 轴的距离等
轴的距离等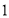 B.
B.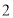 C.
C.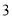 D.
D.
 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线 的焦点重合,
的焦点重合, 的值为 .
的值为 . 且
且 
 的最小正值及此时函数
的最小正值及此时函数 的表达式;
的表达式; 的图象;
的图象;