题目内容
(1)求 的最小正值及此时函数
的最小正值及此时函数 的表达式;
的表达式;
(2)将(1)中所得函数 的图象结果怎样的变换可得
的图象结果怎样的变换可得 的图象;
的图象;
(1)1, ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)由 得
得 ,于是
,于是 ,即
,即 ,故当
,故当 时,
时, 取得最小正值1,此时
取得最小正值1,此时 ;(2)三角函数的图像变换可以先平移再伸缩,也可以先伸缩再平移.详见解析(2).
;(2)三角函数的图像变换可以先平移再伸缩,也可以先伸缩再平移.详见解析(2).
试题解析:(1)因为 ,所以
,所以 ,
,
于是 ,即
,即 ,故当
,故当 时,
时, 取得最小正值1,此时
取得最小正值1,此时 ;
;
(2)(方法一)先将 的图象向右平移
的图象向右平移 个单位,得
个单位,得 的图象;
的图象;
再将所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得 的图象;
的图象;
最后将所得图象上各点的纵坐标缩小到原来的 倍(横坐标不变),得
倍(横坐标不变),得 的图象
的图象
(方法二)先将 的图象各点的横坐标伸长到原来的2倍(纵坐标不变),得
的图象各点的横坐标伸长到原来的2倍(纵坐标不变),得 的图象;再将所得图象向右平移
的图象;再将所得图象向右平移 个单位得
个单位得 的图象;最后将所得图象上各点的纵坐标缩小到原来的
的图象;最后将所得图象上各点的纵坐标缩小到原来的 倍(横坐标不变),得
倍(横坐标不变),得 的图象.
的图象.
考点:(1)用待定系数法求函数解析式;(2)三角函数的图像变换.

练习册系列答案
相关题目
 且
且 
 、离心率为
、离心率为 ,直线
,直线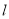 与y轴交于点P(0,
与y轴交于点P(0,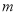 ),与椭圆C交于相异两点A、B,且
),与椭圆C交于相异两点A、B,且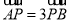 。
。 为等差数列,
为等差数列, 为其前
为其前 项和.若
项和.若 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 的右焦点与抛物线
的右焦点与抛物线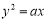 的焦点重合,则该抛物线的准线被双曲线所截的线段长度为( )
的焦点重合,则该抛物线的准线被双曲线所截的线段长度为( )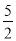 D.
D.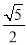
 :
: ,
, ,那么命题
,那么命题 为( )
为( ) B.
B.
 D.
D.
 的近似解在区间
的近似解在区间 ,则
,则 .
. 的值域为 .
的值域为 . 的图像如左图所示,那么函数
的图像如左图所示,那么函数 的图像最有可能的是
的图像最有可能的是 
 中,
中, 分别为
分别为 中点,则异面直线
中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为
 B.
B. C.
C. D.
D.