题目内容

设x，y，z＞0，则三个数 
y
x
+
y
z
，
z
x
+
z
y
，
x
z
+
x
y
（　　）
A、都大于2
B、至少有一个大于2
C、至少有一个不小于2
D、至少有一个不大于2
分析：假设：
y
x
+
y
z
，
z
x
+
z
y
，
x
z
+
x
y
中都小于2，则
y
x
+
y
z
+
z
x
+
z
y
+
x
z
+
x
y
＜6，但由于
y
x
+
y
z
+
z
x
+
z
y
+
x
z
+
x
y
=(
y
x
+
x
y
)+(
z
x
+
x
z
)+(
y
z
+
z
y
)≥2+2+2=6，出现矛盾，从而得出正确答案：
y
x
+
y
z
，
z
x
+
z
y
，
x
z
+
x
y
中至少有一个不小于2．
解答：解：由于
y
x
+
y
z
+
z
x
+
z
y
+
x
z
+
x
y
=(
y
x
+
x
y
)+(
z
x
+
x
z
)+(
y
z
+
z
y
)≥2+2+2=6，
∴
y
x
+
y
z
，
z
x
+
z
y
，
x
z
+
x
y
中至少有一个不小于2，
故选C．
点评：分析法──通过对事物原因或结果的周密分析，从而证明论点的正确性、合理性的论证方法，也称为因果分析，从求证的不等式出发，“由果索因”，逆向逐步找这个不等式成立需要具备的充分条件；综合法是指从已知条件出发，借助其性质和有关定理，经过逐步的逻辑推理，最后达到待证结论或需求问题，其特点和思路是“由因导果”，即从“已知”看“可知”，逐步推向“未知”．
练习册系列答案
相关题目
设x，y，z∈（0，1），且x+y+z=2，设u=xy+yz+zx，则u的最大值为
4
3
4
3
．
设x，y，z∈（0，+∞），则三数x+
1
y
，y+
1
z
，z+
1
x
中（　　）
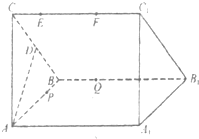（2012•成都一模）设直三梭柱ABC-A1B1C1的底面为等腰直角三角形，AB=AC=2，动点E、F在侧棱CC1上，动点P、Q分别碰AB1，BB1上，若EF═1，CE=x，BQ=y，BP=z，其中x，y，z＞0，则下列结论中错误的是．（　　）
设x，y，z＞0，则三个数 
y
x
+
y
z
，
z
x
+
z
y
，
x
z
+
x
y
（　　）
A．都大于2B．至少有一个大于2
C．至少有一个不小于2D．至少有一个不大于2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网