题目内容
已知数列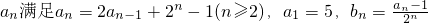 .
.
(Ⅰ)证明:{bn}为等差数列;
(Ⅱ)求数列{an}的前n项和Sn;
(Ⅲ)设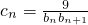 ,求数列{cn}的前n项和Tn,并求使
,求数列{cn}的前n项和Tn,并求使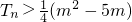 对所有的n∈N*都成立的最大正整数m的值.
对所有的n∈N*都成立的最大正整数m的值.
解:(Ⅰ)证明:∵ =
=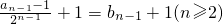 ,
,
∴bn-bn-1=1(n≥2),
∴{bn}是公差为1,首项为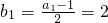 的等差数列…(4分)
的等差数列…(4分)
(Ⅱ)解:由(Ⅰ)知bn=2+(n-1)•1=n+1,
即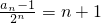 ,
,
∴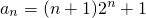 ,
,
∴ ,…(6分)
,…(6分)
令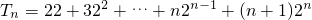 ,
,
∴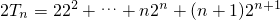 ,
,
∴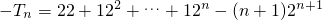 =
=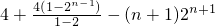 =4+2n+1-4-n•2n+1-2n+1=-n•2n+1,
=4+2n+1-4-n•2n+1-2n+1=-n•2n+1,
∴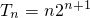 ,∴
,∴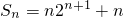 .…(9分)
.…(9分)
(Ⅲ)由(Ⅰ)知,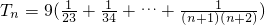
= …(12分)
…(12分)
∴ ,
,
依题意有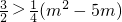 ,
,
解得-1<m<6,
故所求最大正整数m的值为5…(14分)
分析:(I)由已知中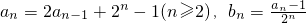 ,化简可得bn-bn-1=1,进而根据等差数列的定义可得结论
,化简可得bn-bn-1=1,进而根据等差数列的定义可得结论
(II)由(I)求出数列{an}的通项公式,进而利用错位相减法,可得答案.
(III)结合(I)的结论,求出数列{cn}的通项公式,进而利用裂项相消法,求出数列{cn}的前n项和Tn,进而求出m的值,
点评:本题考查的知识点是数列求和,数列的应用及等差关系的确定,其中(I)的关键是熟练掌握定义法求证等差数列的步骤,(II)(III)的关键是熟练掌握错位相减法和裂项相消法的适用范围及方法步骤.
 =
=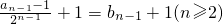 ,
,∴bn-bn-1=1(n≥2),
∴{bn}是公差为1,首项为
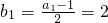 的等差数列…(4分)
的等差数列…(4分)(Ⅱ)解:由(Ⅰ)知bn=2+(n-1)•1=n+1,
即
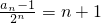 ,
,∴
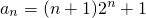 ,
,∴
 ,…(6分)
,…(6分)令
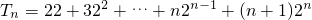 ,
,∴
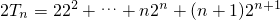 ,
,∴
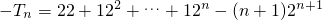 =
=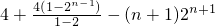 =4+2n+1-4-n•2n+1-2n+1=-n•2n+1,
=4+2n+1-4-n•2n+1-2n+1=-n•2n+1,∴
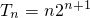 ,∴
,∴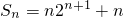 .…(9分)
.…(9分)(Ⅲ)由(Ⅰ)知,
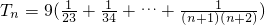
=
 …(12分)
…(12分)∴
 ,
,依题意有
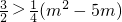 ,
,解得-1<m<6,
故所求最大正整数m的值为5…(14分)
分析:(I)由已知中
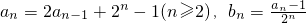 ,化简可得bn-bn-1=1,进而根据等差数列的定义可得结论
,化简可得bn-bn-1=1,进而根据等差数列的定义可得结论(II)由(I)求出数列{an}的通项公式,进而利用错位相减法,可得答案.
(III)结合(I)的结论,求出数列{cn}的通项公式,进而利用裂项相消法,求出数列{cn}的前n项和Tn,进而求出m的值,
点评:本题考查的知识点是数列求和,数列的应用及等差关系的确定,其中(I)的关键是熟练掌握定义法求证等差数列的步骤,(II)(III)的关键是熟练掌握错位相减法和裂项相消法的适用范围及方法步骤.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 满足
满足
 是等比数列;
是等比数列; 满足
满足 证明
证明 }满足
}满足 .
. }满足
}满足 ,设
,设 是数列
是数列 的前n项和.
的前n项和.