题目内容
下列求导运算正确的是( )A.(x2cos x)′=-2xsin
B.(x+
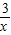 )′=1+
)′=1+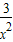
C.(log2x)′=
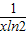
D.(3x)′=3xlog3e
【答案】分析:利用基本初等函数的导数公式、导数的运算法则对给出的四种运算逐一验证,即可得到正确答案.
解答:解:因为(x2cos x)′=2xcos x+x2(-sinx),所以选项A不正确;
(x+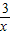 )′=1-
)′=1-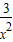 ,所以选项B不正确;
,所以选项B不正确;
(log2x)′=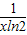 ,所以选项C正确;
,所以选项C正确;
(3x)′=3xloge3,所以选项D不正确.
故选C.
点评:本题考查了简单的复合函数的导数,解答的关键是熟记基本初等函数的导数公式,此题是基础题.
解答:解:因为(x2cos x)′=2xcos x+x2(-sinx),所以选项A不正确;
(x+
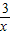 )′=1-
)′=1-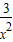 ,所以选项B不正确;
,所以选项B不正确;(log2x)′=
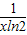 ,所以选项C正确;
,所以选项C正确;(3x)′=3xloge3,所以选项D不正确.
故选C.
点评:本题考查了简单的复合函数的导数,解答的关键是熟记基本初等函数的导数公式,此题是基础题.

练习册系列答案
相关题目
下列求导运算正确的是( )
A、(
| ||||
B、(
| ||||
| C、(x2cosx)′=-2xsinx | ||||
D、(log2x)′=
|
下列求导运算正确的是( )
A、(log3x)′=
| ||||
B、(x+
| ||||
| C、(5x)′=5xlog5e | ||||
| D、(x2cosx)′=2xsinx |