题目内容
已知数列{an}满足:a1=
,an+1=an2+an,则
+
+
+…+
的值所在区间是( )
| 1 |
| 2 |
| 1 |
| a1+1 |
| 1 |
| a2+1 |
| 1 |
| a3+1 |
| 1 |
| a2014+1 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
考点:数列递推式,数列的求和
专题:点列、递归数列与数学归纳法
分析:根据数列的递推关系得到
=
-
,利用裂项法进行求和,即可得到结论.
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| an+1-1 |
解答:
解:由an+1=an2+an,
得an+1=an(an+1),
取倒数得
=
=
-
,
则
=
-
,
即m=
+
+…+
=
+
-
+
-
+…+
-
=4-
,
∵an+1=an2+an>an,
∴
<
∴1<
<
<…<
=2,
即-1>-
>-2,
则3>4-
>2,
即2<m<3
故m所在的区间为(2,3),
故选:C
得an+1=an(an+1),
取倒数得
| 1 |
| an+1 |
| 1 |
| an(an+1) |
| 1 |
| an |
| 1 |
| an+1 |
则
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an+1 |
即m=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2013 |
| 1 |
| a1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2014 |
| 1 |
| a2015 |
| 1 |
| a2015 |
∵an+1=an2+an>an,
∴
| 1 |
| an+1 |
| 1 |
| an |
∴1<
| 1 |
| a2015 |
| 1 |
| a2014 |
| 1 |
| a1 |
即-1>-
| 1 |
| a2015 |
则3>4-
| 1 |
| a2015 |
即2<m<3
故m所在的区间为(2,3),
故选:C
点评:本题主要考查递推数列的应用.根据递推公式求出
=
-
是解决本题的关键.难度较大.
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an+1 |

练习册系列答案
相关题目
在下列幂函数中,过点(0,0)和(-1,1),并且是偶函数的是( )
| A、y=-x | ||
| B、y=x-2 | ||
C、y=x
| ||
D、y=x
|
已知函数f(x)=
,若函教f(x)的值域是[-1,1],则实数k的取值范围是( )
|
| A、[-1,0] | ||
B、[0,
| ||
C、[
| ||
D、[1,
|
设a,b,c均为正数,且(
)a=log2a,(
)b=log
b,2c=log
c,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<a<c |
在△ABC中,已知
•
=tanA,当A=
时,△ABC的面积为( )
| AB |
| AC |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
等差数列{an}满足a7+a8+a3=15,函数fn(x)=sin(
x+
),那么f5(a6)的值为( )
| π |
| n |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
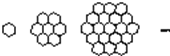 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数.