题目内容
设抛物线过定点A(-1,0),且以直线x=1为准线
(Ⅰ)求抛物线顶点的轨迹C的方程;
(Ⅱ)若直线l与轨迹C交于不同的两点M,N,且线段MN恰被直线x=- 平分,设弦MN的垂直平分线的方程为y=kx+m,试求m的取值范围
平分,设弦MN的垂直平分线的方程为y=kx+m,试求m的取值范围
 解:(Ⅰ)设抛物线的顶点为G(x,y),则其焦点为F(2x-1,y)由抛物线的定义可知:|AF|=点A到直线x=1的距离为2,
解:(Ⅰ)设抛物线的顶点为G(x,y),则其焦点为F(2x-1,y)由抛物线的定义可知:|AF|=点A到直线x=1的距离为2,所以,
 =2
=2所以,抛物线顶点G的轨迹C的方程为x2+
 =1(x≠1)
=1(x≠1)(Ⅱ)显然,直线l与坐标轴不可能平行,所以,设直线l的方程为y=-
 x+b,
x+b,代入椭圆方程得:
 x2-
x2- +b2-4=0
+b2-4=0由于l与轨迹C交于不同的两点M,N,所以,△=
 -4(
-4( )(b2-4)>0,即4k2-k2b2+1>0(k≠0)(*)
)(b2-4)>0,即4k2-k2b2+1>0(k≠0)(*)又线段MN恰被直线x=-
 平分,所以,xM+xN=
平分,所以,xM+xN= =2×(-
=2×(- )
)所以bk=
 ,代入(*)可解得:-
,代入(*)可解得:- <k<
<k< (k≠0)
(k≠0)由于y=kx+m为弦MN的垂直平分线,故可考虑弦MN的中点P(-
 ,y0)
,y0)在y=-
 x+b,中,令x=-
x+b,中,令x=- ,可解得:y0=-
,可解得:y0=- +b=-2k
+b=-2k将点P(-
 -2k)代入y=kx+m,可得:m=-
-2k)代入y=kx+m,可得:m=- k
k所以-
 m<
m< ,m≠0
,m≠0分析:(Ⅰ)设抛物线的顶点为G,则焦点坐标可得,进而根据抛物线的定义可知:|AF|=点A到直线x=1的距离进而利用两点间的距离公式求得x和y的关系式求得抛物线顶点G的轨迹C的方程.
(Ⅱ)因为m是弦MN的垂直平分线与y轴交点的纵坐标,由MN所唯一确定所以,要求m的取值范围,还应该从直线l与轨C相交入手
设直线l的方程与轨迹C的方程联立消去y,根据判别式大于0求得k的不等式方程,进而根据线段MN恰被直线x=-
 平分,求得xM+xN的表达式,进而求得bk,带代入到判别式求得k的范围,下面只需找到m与k的关系,即可求出m的取值范围.求得MN中点P的坐标,把x=-
平分,求得xM+xN的表达式,进而求得bk,带代入到判别式求得k的范围,下面只需找到m与k的关系,即可求出m的取值范围.求得MN中点P的坐标,把x=- 代入即可求得y0的表达式,将P点坐标代入直线方程求得k和m的关系式,进而根据m的范围求得k的范围.
代入即可求得y0的表达式,将P点坐标代入直线方程求得k和m的关系式,进而根据m的范围求得k的范围.点评:本题主要考查了抛物线的简单性质.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
相关题目
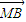 •
•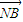 =0的M、N两点?证明你的结论.
=0的M、N两点?证明你的结论.