题目内容
设抛物线过定点A(2,0),且以直线x=-2为准线.
(1)求抛物线顶点的轨迹C的方程;
(2)已知点B(0,-5),轨迹C上是否存在满足
•
=0的M、N两点?证明你的结论.
(1)求抛物线顶点的轨迹C的方程;
(2)已知点B(0,-5),轨迹C上是否存在满足
| MB |
| NB |
(1)设抛物线顶点P(x,y),则抛物线的焦点F(2x+2,y),
由抛物线的定义可得
=4.
∴
+
=1.
∴轨迹C的方程为
+
=1(x≠2).
(2)不存在.证明如下:
过点B(0,-5)斜率为k的直线方程为y=kx-5(斜率不存在时,显然不符合题意),
由
得(4+k2)x2-10kx+9=0,
由△≥0得k2≥
.
假设在轨迹C上存在两点M、N,令MB、NB的斜率分别为k1、k2,则|k1|≥
,|k2|≥
,显然不可能满足k1•k2=-1,
∴轨迹C上不存在满足
•
=0的两点.
由抛物线的定义可得
| (2x+2-2)2+y2 |
∴
| x2 |
| 4 |
| y2 |
| 16 |
∴轨迹C的方程为
| x2 |
| 4 |
| y2 |
| 16 |
(2)不存在.证明如下:
过点B(0,-5)斜率为k的直线方程为y=kx-5(斜率不存在时,显然不符合题意),
由
|
由△≥0得k2≥
| 9 |
| 4 |
假设在轨迹C上存在两点M、N,令MB、NB的斜率分别为k1、k2,则|k1|≥
| 3 |
| 2 |
| 3 |
| 2 |
∴轨迹C上不存在满足
| MB |
| NB |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 •
• =0的M、N两点?证明你的结论.
=0的M、N两点?证明你的结论.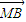 •
•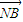 =0的M、N两点?证明你的结论.
=0的M、N两点?证明你的结论.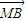 •
•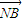 =0的M、N两点?证明你的结论.
=0的M、N两点?证明你的结论.