题目内容
设椭圆M: (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4.(1)求椭圆M的方程;
(2)若直线y=
 x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值.
【答案】分析:(1)由于双曲线的离心率为 ,可得椭圆的离心率,又圆x2+y2=4的直径为4,则2a=4,从而列出关于a,b,c的方程求得a,b,c.最后写出椭圆M的方程;
,可得椭圆的离心率,又圆x2+y2=4的直径为4,则2a=4,从而列出关于a,b,c的方程求得a,b,c.最后写出椭圆M的方程;
(2)直线AB的直线方程: .将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得△PAB面积的最大值,从而解决问题.
.将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得△PAB面积的最大值,从而解决问题.
解答:解:(1)双曲线的离心率为 ,则椭圆的离心率为
,则椭圆的离心率为 (2分)圆x2+y2=4的直径为4,则2a=4,
(2分)圆x2+y2=4的直径为4,则2a=4,
得: ⇒
⇒
所求椭圆M的方程为 .(6分)
.(6分)
(2)直线AB的直线方程: .
.
由 ,得
,得 ,
,
由 ,得-2
,得-2 <m<2
<m<2
∵ ,
, .
.
∴ =
= (9分)
(9分)
又P到AB的距离为 .
.
则
 当且仅当
当且仅当 取等号
取等号
∴ . (12分)
. (12分)
点评:本题主要考查了椭圆的标准方程问题.当研究椭圆和直线的关系的问题时,常可利用联立方程,进而利用韦达定理来解决.
 ,可得椭圆的离心率,又圆x2+y2=4的直径为4,则2a=4,从而列出关于a,b,c的方程求得a,b,c.最后写出椭圆M的方程;
,可得椭圆的离心率,又圆x2+y2=4的直径为4,则2a=4,从而列出关于a,b,c的方程求得a,b,c.最后写出椭圆M的方程;(2)直线AB的直线方程:
 .将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得△PAB面积的最大值,从而解决问题.
.将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得△PAB面积的最大值,从而解决问题.解答:解:(1)双曲线的离心率为
 ,则椭圆的离心率为
,则椭圆的离心率为 (2分)圆x2+y2=4的直径为4,则2a=4,
(2分)圆x2+y2=4的直径为4,则2a=4,得:
 ⇒
⇒
所求椭圆M的方程为
 .(6分)
.(6分)(2)直线AB的直线方程:
 .
.由
 ,得
,得 ,
,由
 ,得-2
,得-2 <m<2
<m<2
∵
 ,
, .
.∴
 =
= (9分)
(9分)又P到AB的距离为
 .
.则

 当且仅当
当且仅当 取等号
取等号∴
 . (12分)
. (12分)点评:本题主要考查了椭圆的标准方程问题.当研究椭圆和直线的关系的问题时,常可利用联立方程,进而利用韦达定理来解决.

练习册系列答案
相关题目
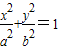 (a>b>0)的离心率为
(a>b>0)的离心率为 ,长轴长为
,长轴长为 ,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.
,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点. ;
; (a>b>0)的离心率为
(a>b>0)的离心率为 ,长轴长为
,长轴长为 ,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.
,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点. ;
; (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4. x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值.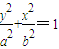 (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4. x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值. (a>b>0)的离心率为
(a>b>0)的离心率为 ,长轴长为
,长轴长为 ,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.
,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.