题目内容

如图,设F1和F2为椭圆b2x2+a2y2=a2b2的两焦点(a＞b＞0),P为椭圆上一点,∠F1PF2=θ,求证:△PF1F2面积S=b2tan.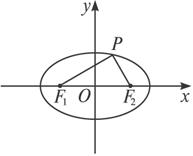

证明:在△PF1F2中,由余弦定理得

|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cosθ=(|PF1|+|PF2|)2-2|PF1|·|PF2|(1+cosθ),

∴(2c)2=(2a)2-2|PF1|·|PF2|(1+cosθ).

∴|PF1|·|PF2|=.

∴S△=|PF1|·|PF2|·sinθ=b2·=b2·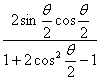=b2tan.

练习册系列答案
相关题目
（2012•重庆）如图，设椭圆的中心为原点O，长轴在x轴上，上顶点为A，左右焦点分别为F1，F2，线段OF1，OF2的中点分别为B1，B2，且△AB1B2是面积为4的直角三角形．
（Ⅰ）求该椭圆的离心率和标准方程；
（Ⅱ）过B1做直线l交椭圆于P，Q两点，使PB2⊥QB2，求直线l的方程．
（2012•重庆）如图，设椭圆的中心为原点O，长轴在x轴上，上顶点为A，左、右焦点分别为F1，F2，线段OF1，OF2的中点分别为B1，B2，且△AB1B2是面积为4的直角三角形．
（Ⅰ）求该椭圆的离心率和标准方程；
（Ⅱ）过B1作直线交椭圆于P，Q两点，使PB2⊥QB2，求△PB2Q的面积．

如图，设F1、F2分别为椭圆C：(a＞b＞0)的左、右焦点．

(1)设椭圆C上的点到F1、F2两点距离之和等于4，求椭圆C的方程和离心率；

(2)设点K是(1)中所得椭圆上的动点，求线段F1K的中点的轨迹方程．

如图，设椭圆的中心为原点O，长轴在x轴上，上顶点为A，左、右焦点分别为F1，F2，线段OF1，OF2的中点分别为B1，B2，且△AB1B2是面积为4的直角三角形．

(1)求该椭圆的离心率和标准方程；

(2)过B1作直线l交椭圆于P，Q两点，使PB2⊥QB2，求直线l的方程．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网