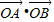Question

已知△ABC内接于以O为圆心，以1为半径的圆，且3

OA

+4

OB

+5

OC

=

O

，
（Ⅰ）求数量积

OA

•

OB

（Ⅱ）求△ABC面积．

Answer 1

分析：（1）先根据向量的数量积运算对所求的式子移到右面一项后两边同时平方可求．
（2）由（1）可知OA⊥OB得然后以O为原点，

OA

，

OB

为x，y轴建立平面直角坐标系，设出C的坐标，表示出 

OA

，

OB

，

OC

进而可求出C的坐标，最后根据S=S_△AOB+S_△AOC+S_△BOC可求出答案．

解答：解：（1）∵3

OA

+4

OB

+5

OC

=

O

，且外接圆的半径r=1，
∴(3

OA

+4

OB

)2=(-5

OC

) 2=25．
∴9+16+24

OA

•

OB

=25，
∴

OA

•

OB

=0，
同理可得，

OC

•

OB

=-

4

5

，

OC

•

OA

=-

3

5

．
（2）设C（m，n）则3（1，0）+4（0，1）+5（m，n）=0．
解得m=-

3

5

，n=-

4

5

S=S_△AOB+S_△AOC+S_△BOC
=

1

2

OA•OB+

1

2

OA•n+

1

2

OB•m
=

1

2

×1×1+

1

2

×1×

4

5

+

1

2

×1×

3

5

=

6

5

．

点评：本题主要考查向量的数量积运算和三角形的面积公式．三角函数和向量的综合题是高考的重点和热点，要给予重视．