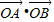Question

已知△ABC内接于以O为圆心，1为半径的圆，且3

OA

+4

OB

+5

OC

=

0

，则

OC

•

AB

=

-

1

5

．

Answer 1

分析：利用向量条件先求得

OA

•

OB

=0，再把所求式转化为(-

3

5

OA

-

4

5

OB

)•(

OB

-

OA

)，利用数量积公式，即可得到结论．

解答：解：由题意，|OA|=|OB|=|OC|=1
∵3

OA

+4

OB

+5

OC

=

0

，
∴3

OA

+4

OB

=-5

OC

，两边平方得  9+24

OA

•

OB

+16=25，
∴

OA

•

OB

=0
∵3

OA

+4

OB

=-5

OC

∴

OC

=-

3

5

OA

-

4

5

OB

∴

OC

•

AB

=(-

3

5

OA

-

4

5

OB

)•(

OB

-

OA

)=

3

5

-

4

5

=-

1

5

故答案为：-

1

5

点评：本题考查向量的线性运算，考查向量的数量积，考查向量的垂直，解题的关键是把所求式转化为(-

3

5

OA

-

4

5

OB

)•(

OB

-

OA

)，利用数量积公式求解．