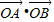题目内容
已知△ABC内接于以0为圆心，1为半径的圆，且3•| OA |
| OB |
| OC |
| 0 |
分析：先根据向量的数量积运算得到|
|和
⊥
，然后以O为原点，
，
为x，y轴建立平面直角坐标系，设出C的坐标，表示出
、
、
，进而可求出C的坐标，最后根据S=S△oab+S△obc+S△oac可求出答案．
| OC |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| OC |
解答：解：（3
+4
）2=9+16+24
•
=（-5
）2=25．
则：
•
=0，
⊥
．
以O为原点，
，
为x，y轴建立平面直角坐标系，设C坐标为（u，v）
∴3（1，0）+4（0，1）+5（u，v）=0．
u=-
，v=-
．
S=S△oab+S△obc+S△oac=
故答案为：
．
| OA |
| OB |
| OA |
| OB |
| OC |
则：
| OA |
| OB |
| OA |
| OB |
以O为原点，
| OA |
| OB |
∴3（1，0）+4（0，1）+5（u，v）=0．
u=-
| 3 |
| 5 |
| 4 |
| 5 |
S=S△oab+S△obc+S△oac=
| 6 |
| 5 |
故答案为：
| 6 |
| 5 |
点评：本题主要考查向量的数量积运算和三角形的面积公式．三角函数和向量的综合题是高考的重点，每年必考，要给予重视．
练习册系列答案
相关题目
，