题目内容
设椭圆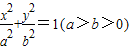 的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过N点作直线l交椭圆于A、B两点.
的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过N点作直线l交椭圆于A、B两点.(1)求椭圆的方程;
(2)若以AB为直径的圆过点F1,试求直线l的方程.
【答案】分析:(1)根据题设知c=2,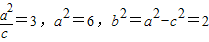 ,由此能求出椭圆方程.
,由此能求出椭圆方程.
(2)当直线AB⊥x轴时,设AB的方程为y=k(x+3),由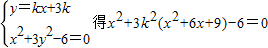 ,然后由韦达定理结合题设条件进行求解.
,然后由韦达定理结合题设条件进行求解.
解答:解:(1)c=2,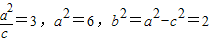
∴椭圆方程为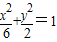 (4分)
(4分)
(2)当直线AB⊥x轴时,
与椭圆无公共点,∴可设AB的方程为y=k(x+3)
由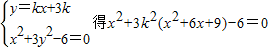
即(3k2+1)x2+18k2x+27k2-6=0①
设A(x1,y1),B(x2,y2),则有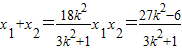 (4分)
(4分)
依题设有,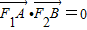
即(x1+2)(x2+2)+y1y2=0(2分)x1x2+2(x1+x2)+4+k2[x1x2+3(x1+x2)+9]=0(k2+1)x1x2+(3k2+2)(x1+x2)+9k2+4=0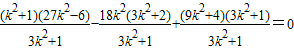
 (4分)
(4分)
将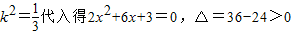
∴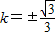 时问题的解
时问题的解
∴AB的方程为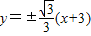 (2分)
(2分)
点评:本题考查直线和圆锥曲线的综合运用,解题时要认真审题,合理地进行等价转化,注意挖掘题设中的隐含条件.
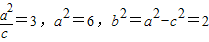 ,由此能求出椭圆方程.
,由此能求出椭圆方程.(2)当直线AB⊥x轴时,设AB的方程为y=k(x+3),由
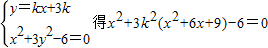 ,然后由韦达定理结合题设条件进行求解.
,然后由韦达定理结合题设条件进行求解.解答:解:(1)c=2,
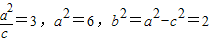
∴椭圆方程为
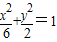 (4分)
(4分)(2)当直线AB⊥x轴时,
与椭圆无公共点,∴可设AB的方程为y=k(x+3)
由
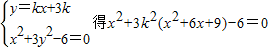
即(3k2+1)x2+18k2x+27k2-6=0①
设A(x1,y1),B(x2,y2),则有
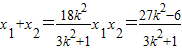 (4分)
(4分)依题设有,
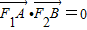
即(x1+2)(x2+2)+y1y2=0(2分)x1x2+2(x1+x2)+4+k2[x1x2+3(x1+x2)+9]=0(k2+1)x1x2+(3k2+2)(x1+x2)+9k2+4=0
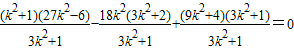
 (4分)
(4分)将
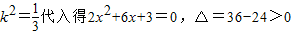
∴
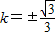 时问题的解
时问题的解∴AB的方程为
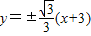 (2分)
(2分)点评:本题考查直线和圆锥曲线的综合运用,解题时要认真审题,合理地进行等价转化,注意挖掘题设中的隐含条件.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 的离心率为
的离心率为 ,
, 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. 过点F1,且垂直于椭圆的长轴,动直线
过点F1,且垂直于椭圆的长轴,动直线 垂直
垂直 的离心率为
的离心率为 ,
, 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. 过点F1,且垂直于椭圆的长轴,动直线
过点F1,且垂直于椭圆的长轴,动直线 垂直
垂直 的离心率为
的离心率为 ,
, 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切。
的短半轴长为半径的圆相切。 过点F1,且垂直于椭圆的长轴,动直
过点F1,且垂直于椭圆的长轴,动直 垂直
垂直 的离心率为
的离心率为 ,
, 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切。
的短半轴长为半径的圆相切。 过点F1,且垂直于椭圆的长轴,动直
过点F1,且垂直于椭圆的长轴,动直 垂直
垂直