题目内容
(09年滨州一模理)(12分)
设函数![]()
(I)若直线l与函数![]() 的图象都相切,且与函数
的图象都相切,且与函数![]() 的图象相切于点
的图象相切于点
(1,0),求实数p的值;
(II)若![]() 在其定义域内为单调函数,求实数p的取值范围;
在其定义域内为单调函数,求实数p的取值范围;
解析:(Ⅰ)方法一:∵![]() ,
,
∴![]() .
.
设直线![]() ,
,
并设l与g(x)=x2相切于点M(![]() )
)
∵![]()
![]() ∴2
∴2![]()
∴![]()
代入直线l方程解得p=1或p=3.
方法二:
将直线方程l代入 ![]() 得
得
![]()
∴![]()
解得p=1或p=3 .
(Ⅱ)∵![]() ,
,
①要使![]() 为单调增函数,须
为单调增函数,须![]() 在
在![]() 恒成立,
恒成立,
即![]() 在
在![]() 恒成立,即
恒成立,即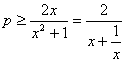 在
在![]() 恒成立,
恒成立,
又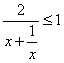 ,所以当
,所以当![]() 时,
时,![]() 在
在![]() 为单调增函数; …………6分
为单调增函数; …………6分
②要使![]() 为单调减函数,须
为单调减函数,须![]() 在
在![]() 恒成立,
恒成立,
即![]() 在
在![]() 恒成立,即
恒成立,即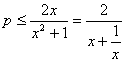 在
在![]() 恒成立,
恒成立,
又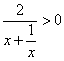 ,所以当
,所以当![]() 时,
时,![]() 在
在![]() 为单调减函数.
为单调减函数.
综上,若![]() 在
在![]() 为单调函数,则
为单调函数,则![]() 的取值范围为
的取值范围为![]() 或
或![]() .………8分
.………8分

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
